Matlab Tutorial - Introduction to FFT & DFT
A Fast Fourier transform (FFT) is a fast computational algorithm to compute the discrete Fourier transform (DFT) and its inverse. The Fast Fourier Transform does not refer to a new or different type of Fourier transform. It refers to a very efficient algorithm for computing the DFT.
The time takes to perform a DFT on a computer depends primarily on the number of multiplications involved ($O (N^2))$ while FFT only needs $Nlog_2(N)$.
The central insight which leads to this algorithm is the realization that a discrete Fourier transform of a sequence of $N$ points can be written in terms of two discrete Fourier transforms of length $N/2$. Therefore, if $N$ is a power of 2, it is possible to recursively apply this decomposition.
Here are the functions related to FFT and DFT. The cases actually using these functions are in other pages.
- The function $dft()$ computes the discrete Fourier transform. Define a vector $x$ and compute the DFT using the command:
X = dft(x)
The first element in $X$ corresponds to the value of $X(0)$. - $idft()$ computes the inverse discrete Fourier transform. Define a vector $X$ and compute the IDFT using the command
x = idft(X)
The first element of the resulting vector $x$ is $x[0]$. - For a more efficient but less obvious program, the discrete Fourier transform can be computed using the function $fft()$ which performs a Fast Fourier Transform of a sequence of numbers. To compute the FFT of a sequence $x[n]$ which is stored in the vector $x$, use the command
X = fft(x)
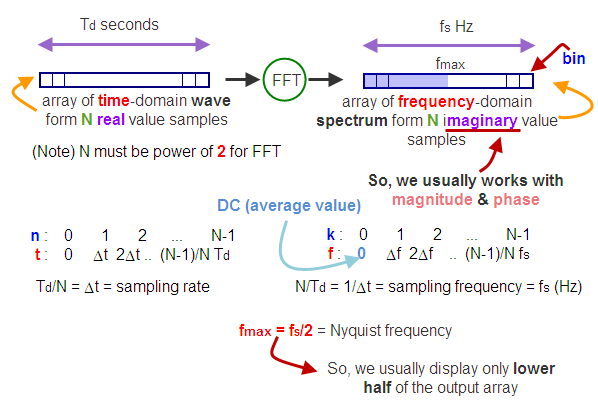
If we use this way, the $fft()$ is interchangeable with the command $dft()$. For more computational efficiency, the length of the vector $x$ should be equal to the power of 2, that is 64, 128, 512, etc. The vector $x$ can be padded with zeros to make it have an appropriate length. MATLAB does this automatically by using the following command where $N$ is defined to be an power of 2:X = fft(x,N);
The longer the length of $x$, the finer the grid will be for the FFT. Due to a wrap around effect, only the first $N/2$ points of the FFT have any meaning. - The $ifft()$ function computes the inverse Fourier transform:
x = ifft(X);
-
The FFT can be used to approximate the Fourier transform of a continuous-time signal. A continuous-time signal $x(t)$ is sampled with a period of $T$ seconds, then the DFT is computed for the sampled signal. The resulting amplitude must be scaled and the corresponding frequency determined. An M-file that approximates the Fourier Transform of a sampled continuous-time signal can be downloaded from contfft.m. Let a vector $x $be defined as the sampled continuous-time signal $x(t)$ and let $T$ be the sampling time.
[X,w] = contfft(x,T);
The outputs are the Fourier transform stored in the vector $X$ and the corresponding frequency vector $w$.
Ph.D. / Golden Gate Ave, San Francisco / Seoul National Univ / Carnegie Mellon / UC Berkeley / DevOps / Deep Learning / Visualization