Single Layer Neural Network : Adaptive Linear Neuron using linear (identity) activation function with batch gradient method

bogotobogo.com site search:

Note

In this tutorial, we'll learn another type of single-layer neural network (still this is also a perceptron) called Adaline (Adaptive linear neuron) rule (also known as the Widrow-Hoff rule).

The key difference between the Adaline rule (also known as the Widrow-Hoff rule) and Rosenblatt's perceptron is that the weights are updated based on a linear activation function rather than a unit step function like in the Perceptron model.

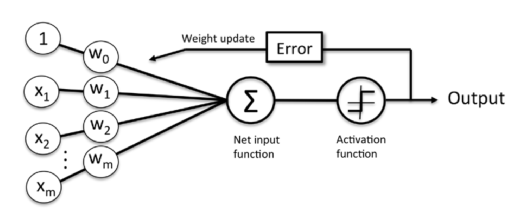
Perceptron

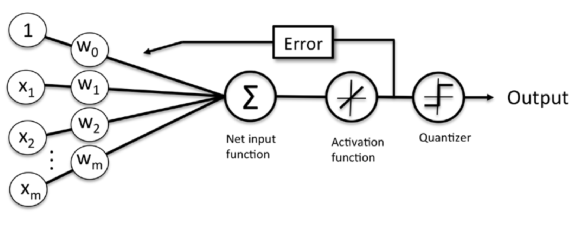
Adaptive linear neuron

The difference is that we're going to use the continuous valued output from the linear activation function to compute the model error and update the weights, rather than the binary class labels.

bogotobogo.com site search:

Artificial neurons

The perceptron algorithm enables the model automatically learn the optimal weight coefficients that are then multiplied with the input features in order to make the decision of whether a neuron fires or not.

In supervised learning and classification, such an algorithm could then be used to predict if a sample belonged to one class or the other.

In binary classifiers perceptron algorithm, we refer to our two classes as either 1 (positive class) or -1 (negative class).

In the context of neural networks, a perceptron is an artificial neuron using the Heaviside step function as the activation function.

The perceptron algorithm is also termed the single-layer perceptron, to distinguish it from a multilayer perceptron. As a linear classifier, the single-layer perceptron is the simplest feedforward neural network.

We can then define an activation function $\phi(z)$ that takes a linear combination of certain input values $x$ and a corresponding weight vector $w$ , where $z$ is the so-called net input ($z = w_1x_1 + ... + w_mx_m$).

$$w=\begin{bmatrix} w_1 \\ . \\ . \\ . \\ w_m \\ \end{bmatrix}, x=\begin{bmatrix} x_1 \\ . \\ . \\ . \\ x_m \\ \end{bmatrix} $$

For our case (binary), we can have:

$$\text if \quad \sum_{i=1}w_ix_i > \theta \quad \text then \quad \phi = 1 $$ $$\text else \quad \sum_{i=1}w_ix_i < \theta \quad \text then \quad \phi = -1 $$

If we set $x_0=1$ and $w_0=-\theta$, we can have more compact form:

$$\text if \quad \sum_{i=0}w_ix_i > 0 \quad \text then \quad \phi(z) = 1 $$ $$\text else \quad \sum_{i=0}w_ix_i < 0 \quad \text then \quad \phi(z) = -1 $$ where $$z=\sum_{i=0}w_ix_i$$

Or more compact form.

Heaviside step activation function:
Linear activation function:

where $\theta$ is a treshold or bias

Updating weights

Update of each weight $w_j$ in the weight vector $w$ can be written as:

$$w_j : = w_j + \Delta w_j$$

The value of $\Delta w_j$ , which is used to update the weight $w_j$, is calculated as the following:

Heaviside step activation function:
Linear activation function:

Cost function

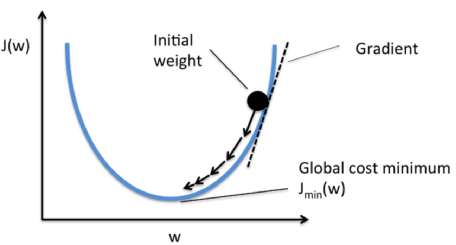
One of the most critical tasks in supervised machine learning algorithms is to minimize cost function.

In the case of Adaptive linear neuron, we can define the cost function J to learn the weights as the Sum of Squared Errors (SSE) between the calculated outcome and the true class label:

$$J(w)=\frac{1}{2}\sum_{i}(y^{(i)}-\phi(z^{(i)}))^2$$

COmpared with the unit step function, the advantages of this continuous linear activation function are:

This cost function is differentiable. So, the partial derivative of the SSE cost function with respect to the jth weight is:

where $i$ is the sample # and $j$ is the feature # (dimension of a dataset).

Because it is convex, we can use a simple and powerful, optimization algorithm called gradient descent to find the weights that minimize our cost function to classify the samples in the Iris dataset.

Although the adaptive linear learning rule looks identical to the perceptron rule, the $\phi(z^{(i)})$ with $z^{(i)}=w^Tx^{(i)}$ is a real number and not an integer class label.

Also, the weight update is calculated based on all samples in the training set (instead of updating the weights incrementally after each sample), which is why this approach is also referred to as batch gradient descent.

We can minimize a cost function by taking a step into the opposite direction of a gradient that is calculated from the whole training set, and this is why this approach is also called as batch gradient descent.

Implementation - Adaptive Linear Neuron

Since the perceptron rule and Adaptive Linear Neuron are very similar, we can take the perceptron implementation that we defined earlier and change the fit method so that the weights are updated by minimizing the cost function via gradient descent.

Here is the source code:

import numpy as np

class AdaptiveLinearNeuron(object):
   def __init__(self, rate = 0.01, niter = 10):
      self.rate = rate
      self.niter = niter

   def fit(self, X, y):
      """Fit training data
      X : Training vectors, X.shape : [#samples, #features]
      y : Target values, y.shape : [#samples]
      """

      # weights
      self.weight = np.zeros(1 + X.shape[1])

      # Number of misclassifications
      self.errors = []

      # Cost function
      self.cost = []

      for i in range(self.niter):
         output = self.net_input(X)
         errors = y - output
         self.weight[1:] += self.rate * X.T.dot(errors)
         self.weight[0] += self.rate * errors.sum()
         cost = (errors**2).sum() / 2.0
         self.cost.append(cost)
      return self

   def net_input(self, X):
      """Calculate net input"""
      return np.dot(X, self.weight[1:]) + self.weight[0]

   def activation(self, X):
      """Compute linear activation"""
      return self.net_input(X)

   def predict(self, X):
      """Return class label after unit step"""
      return np.where(self.activation(X) >= 0.0, 1, -1)


import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data', header=None)

y = df.iloc[0:100, 4].values
y = np.where(y == 'Iris-setosa', -1, 1)
X = df.iloc[0:100, [0, 2]].values

fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(8, 4))

# learning rate = 0.01
aln1 = AdaptiveLinearNeuron(0.01, 10).fit(X,y)

ax[0].plot(range(1, len(aln1.cost) + 1), np.log10(aln1.cost), marker='o')
ax[0].set_xlabel('Epochs')
ax[0].set_ylabel('log(Sum-squared-error)')
ax[0].set_title('Adaptive Linear Neuron - Learning rate 0.01')

# learning rate = 0.01
aln2 = AdaptiveLinearNeuron(0.0001, 10).fit(X,y)

ax[1].plot(range(1, len(aln2.cost) + 1), aln2.cost, marker='o')
ax[1].set_xlabel('Epochs')
ax[1].set_ylabel('Sum-squared-error')
ax[1].set_title('Adaptive Linear Neuron - Learning rate 0.0001')
plt.show()

Gradient descent

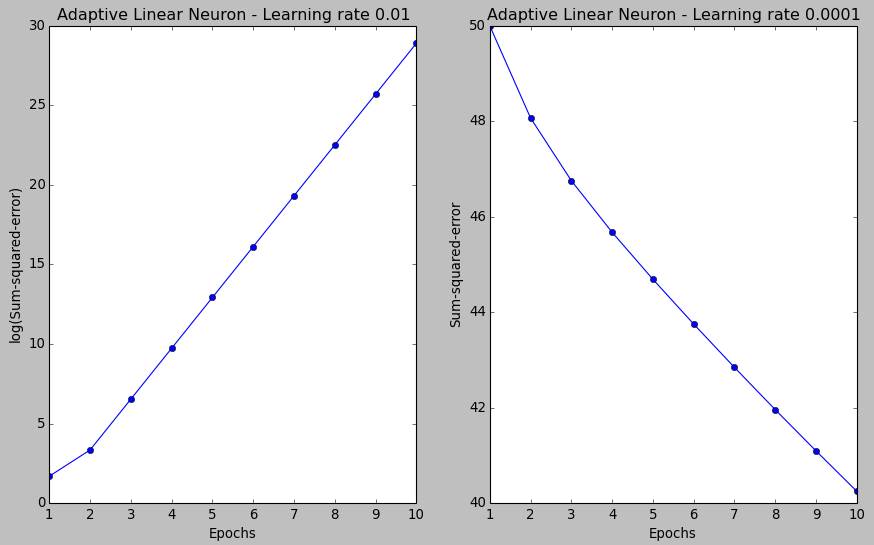
As we can see in the resulting cost function plots below, we have two different types of issues.

The left one shows what could happen if we choose a learning rate that is too large. Instead of minimizing the cost function, the error becomes larger in every epoch because we overshoot the global minimum.

On the other hand, we can see that the cost decreases for the plot on the right side. That's because we chose the learning rate $\eta=0.0001$ is so small that the algorithm would require a very large number of epochs to converge.

The following figure demonstrates how we change the value of a particular weight parameter to minimize the cost function $J$ (left). The figure on the right illustrates what happens if we choose a learning rate that is too large, we overshoot the global minimum:

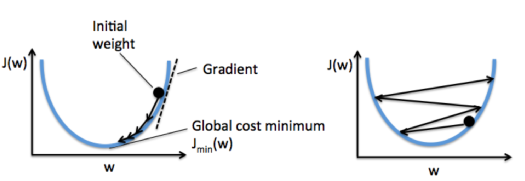
Picture from "Python Machine Learning by Sebastian Raschka, 2015"

Feature scaling

Feature scaling is a method used to standardize the range of independent variables or features of data. In data processing, it is also known as data normalization and is generally performed during the data preprocessing step.

Gradient descent is one of the many algorithms that benefit from feature scaling.

Here, we will use a feature scaling method called standardization, which gives our data the property of a standard normal distribution.

In machine learning, we can handle various types of data, e.g. audio signals and pixel values for image data, and this data can include multiple dimensions.
Feature standardization makes the values of each feature in the data have zero-mean (when subtracting the mean in the enumerator) and unit-variance.
This method is widely used for normalization in many machine learning algorithms (e.g., support vector machines, logistic regression, and neural networks).
This is typically done by calculating standard scores.
The general method of calculation is to determine the distribution mean and standard deviation for each feature. Next we subtract the mean from each feature. Then we divide the values (mean is already subtracted) of each feature by its standard deviation.
- from Feature scaling

So, to standardize the $j$-th feature, we just need to subtract the sample mean $\mu_j$ from every training sample and divide it by its standard deviation $sigma_j$:

$$ x_j^\prime=\frac {x_j-\mu_j}{\sigma_j}$$

where $x_j$ is a vector consisting of the $j$-th feature values of all training samples $n$.

We can standardize by using the NumPy methods mean and std:

X_std = np.copy(X)
X_std[:,0] = (X[:,0] - X[:,0].mean()) / X[:,0].std()
X_std[:,1] = (X[:,1] - X[:,1].mean()) / X[:,1].std()

After the standardization, we will train the Linear model again using the not so small learning rate of $\eta = 0.01$:

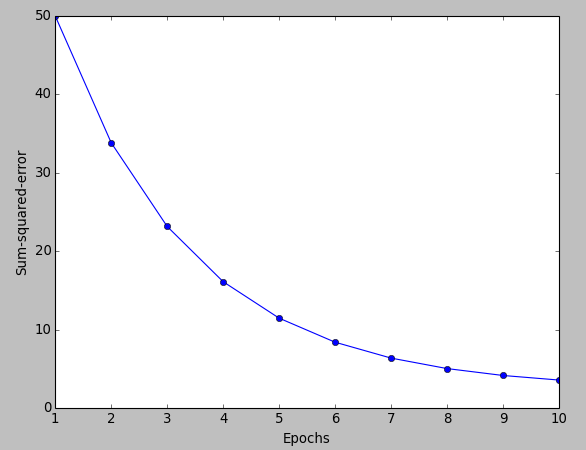
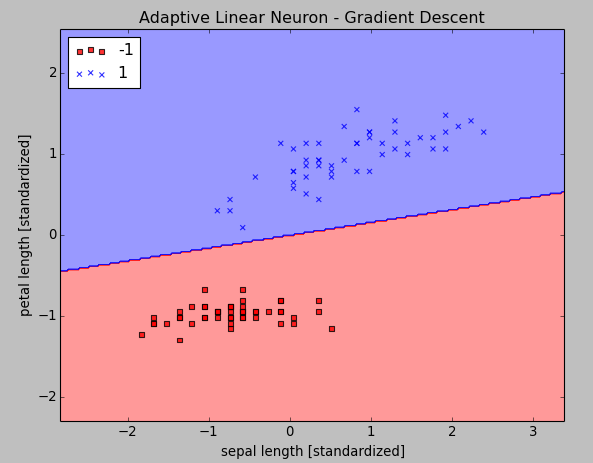
Here is our new code for the two pictures above:

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from matplotlib.colors import ListedColormap

class AdaptiveLinearNeuron(object):
   def __init__(self, rate = 0.01, niter = 10):
      self.rate = rate
      self.niter = niter

   def fit(self, X, y):
      """Fit training data
      X : Training vectors, X.shape : [#samples, #features]
      y : Target values, y.shape : [#samples]
      """

      # weights
      self.weight = np.zeros(1 + X.shape[1])

      # Number of misclassifications
      self.errors = []

      # Cost function
      self.cost = []

      for i in range(self.niter):
         output = self.net_input(X)
         errors = y - output
         self.weight[1:] += self.rate * X.T.dot(errors)
         self.weight[0] += self.rate * errors.sum()
         cost = (errors**2).sum() / 2.0
         self.cost.append(cost)
      return self

   def net_input(self, X):
      """Calculate net input"""
      return np.dot(X, self.weight[1:]) + self.weight[0]

   def activation(self, X):
      """Compute linear activation"""
      return self.net_input(X)

   def predict(self, X):
      """Return class label after unit step"""
      return np.where(self.activation(X) >= 0.0, 1, -1)

def plot_decision_regions(X, y, classifier, resolution=0.02):
   # setup marker generator and color map
   markers = ('s', 'x', 'o', '^', 'v')
   colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
   cmap = ListedColormap(colors[:len(np.unique(y))])

   # plot the decision surface
   x1_min, x1_max = X[:,  0].min() - 1, X[:, 0].max() + 1
   x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
   xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
   np.arange(x2_min, x2_max, resolution))
   Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
   Z = Z.reshape(xx1.shape)
   plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
   plt.xlim(xx1.min(), xx1.max())
   plt.ylim(xx2.min(), xx2.max())

   # plot class samples
   for idx, cl in enumerate(np.unique(y)):
      plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1],
      alpha=0.8, c=cmap(idx),
      marker=markers[idx], label=cl)

df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data', header=None)

y = df.iloc[0:100, 4].values
y = np.where(y == 'Iris-setosa', -1, 1)
X = df.iloc[0:100, [0, 2]].values

# standardize
X_std = np.copy(X)
X_std[:,0] = (X[:,0] - X[:,0].mean()) / X[:,0].std()
X_std[:,1] = (X[:,1] - X[:,1].mean()) / X[:,1].std()

# learning rate = 0.01
aln = AdaptiveLinearNeuron(0.01, 10)
aln.fit(X_std,y)

# decision region plot
plot_decision_regions(X_std, y, classifier=aln)

plt.title('Adaptive Linear Neuron - Gradient Descent')
plt.xlabel('sepal length [standardized]')
plt.ylabel('petal length [standardized]')
plt.legend(loc='upper left')
plt.show()

plt.plot(range(1, len(aln.cost) + 1), aln.cost, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Sum-squared-error')
plt.show()

Continued to Single Layer Neural Network : Adaptive Linear Neuron using linear (identity) activation function with stochastic gradient descent (SGD).