Neural Networks with backpropagation for XOR using one hidden layer

---

---

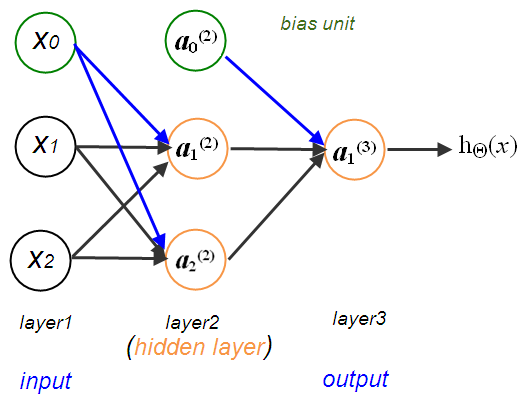
In the picture, we used the following definitions for the notations:

1. $a_i^{(j)}$ : "activation" of unit $i$ in layer $j$
2. $\Theta^{(j)}$ : matrix of weights controlling function mapping from layer $j$ to layer $j+1$

Here are the computations represented by the NN picture above:

$$ a_0^{(2)} = g(\Theta_{00}^{(1)}x_0 + \Theta_{01}^{(1)}x_1 + \Theta_{02}^{(1)}x_2) = g(\Theta_0^Tx) = g(z_0^{(2)}) $$ $$ a_1^{(2)} = g(\Theta_{10}^{(1)}x_0 + \Theta_{11}^{(1)}x_1 + \Theta_{12}^{(1)}x_2) = g(\Theta_1^Tx) = g(z_1^{(2)}) $$ $$ a_2^{(2)} = g(\Theta_{20}^{(1)}x_0 + \Theta_{21}^{(1)}x_1 + \Theta_{22}^{(1)}x_2) = g(\Theta_2^Tx) = g(z_2^{(2)}) $$ $$ h_\Theta(x) = a_1^{(3)}=g(\Theta_{10}^{(2)}a_0^{(2)} + \Theta_{11}^{(2)}a_1^{(2)} + \Theta_{12}^{(2)}a_2^{(2)}) $$

In the equations, the $g$ is sigmoid function that refers to the special case of the logistic function and defined by the formula:

$$ g(z) = \frac{1}{1+e^{-z}} $$

One of the reasons to use the sigmoid function (also called the logistic function) is it was the first one to be used. Its derivative has a very good property. In a lot of weight update algorithms, we need to know a derivative (sometimes even higher order derivatives). These can all be expressed as products of $f$ and $1-f$. In fact, it's the only class of functions that satisfies $f^{'}(t)=f(t)(1-f(t))$.

However, usually the weights are much more important than the particular function chosen. These sigmoid functions are very similar, and the output differences are small. Here's a plot from Wikipedia-Sigmoid function. Note that all functions are normalized in such a way that their slope at the origin is 1.

If we use matrix notation, the equations of the previous section become:

$$ x = \begin{bmatrix} x_0 \\ x_1 \\ x_2 \\ \end{bmatrix} z^{(2)} = \begin{bmatrix} z_0^{(2)} \\ z_1^{(2)} \\ z_2^{(2)} \\ \end{bmatrix} $$ $$ z^{(2)} = \Theta^{(1)}x = \Theta^{(1)}a^{(1)} $$ $$ a^{(2)} = g(z^{(2)}) $$ $$ a_0^{(2)} = 1.0 $$ $$ z^{(3)} = \Theta^{(2)}a^{(2)} $$ $$ h_\Theta(x) = a^{(3)} = g(z^{(3)}) $$

The backpropagation learning algorithm can be divided into two phases: propagation and weight update.
- from wiki - Backpropagatio.

1. Phase 1: Propagation
   Each propagation involves the following steps:
   1. Forward propagation of a training pattern's input through the neural network in order to generate the propagation's output activations.
   2. Backward propagation of the propagation's output activations through the neural network using the training pattern target in order to generate the deltas of all output and hidden neurons.
2. Phase 2: Weight update
   For each weight-synapse follow the following steps:
   1. Multiply its output delta and input activation to get the gradient of the weight.
   2. Subtract a ratio (percentage) of the gradient from the weight.
   This ratio (percentage) influences the speed and quality of learning; it is called the learning rate. The greater the ratio, the faster the neuron trains; the lower the ratio, the more accurate the training is. The sign of the gradient of a weight indicates where the error is increasing, this is why the weight must be updated in the opposite direction.
Repeat phase 1 and 2 until the performance of the network is satisfactory.

If we denote an error of node $j$ in layer $l$ as $\delta_j^{(l)}$, for our output unit(L=3) becomes activation -actual value:

$$ \delta_j^{(3)} = a_j^{(3)} - y_j = h_\Theta(x) - y_j $$

If we use a vector form, it is:

$$ \delta^{(3)} = a^{(3)} - y $$ $$ \delta^{(2)} = (\Theta^{(2)})^T \delta^{(3)} \cdot g^{'}(z^{(2)}) $$ where $$ g^{'}(z^{(2)}) = a^{(2)} \cdot (1-a^{(2)}) $$

Note that we do not have $\delta^{(1)}$ term because that's the input layer and the values are the ones that we observed and they are being used as a training set. So, there is no errors associate with the input.

Also, the derivative of cost function can be written like this:

$$ \frac{\partial}{\partial{\Theta_{ij}^{(l)}}} J(\Theta) = a_j^{(l)}\delta_i^{(l+1)} $$

We use this value to update weights and we can multiply learning rate before we adjust the weight.

self.weights[i] += learning_rate * layer.T.dot(delta)

where the layer in the code is actually $a^{(l)}$.

Source code is here.

import numpy as np

def sigmoid(x):
    return 1.0/(1.0 + np.exp(-x))

def sigmoid_prime(x):
    return sigmoid(x)*(1.0-sigmoid(x))

def tanh(x):
    return np.tanh(x)

def tanh_prime(x):
    return 1.0 - x**2


class NeuralNetwork:

    def __init__(self, layers, activation='tanh'):
        if activation == 'sigmoid':
            self.activation = sigmoid
            self.activation_prime = sigmoid_prime
        elif activation == 'tanh':
            self.activation = tanh
            self.activation_prime = tanh_prime

        # Set weights
        self.weights = []
        # layers = [2,2,1]
        # range of weight values (-1,1)
        # input and hidden layers - random((2+1, 2+1)) : 3 x 3
        for i in range(1, len(layers) - 1):
            r = 2*np.random.random((layers[i-1] + 1, layers[i] + 1)) -1
            self.weights.append(r)
        # output layer - random((2+1, 1)) : 3 x 1
        r = 2*np.random.random( (layers[i] + 1, layers[i+1])) - 1
        self.weights.append(r)

    def fit(self, X, y, learning_rate=0.2, epochs=100000):
        # Add column of ones to X
        # This is to add the bias unit to the input layer
        ones = np.atleast_2d(np.ones(X.shape[0]))
        X = np.concatenate((ones.T, X), axis=1)
         
        for k in range(epochs):
            i = np.random.randint(X.shape[0])
            a = [X[i]]

            for l in range(len(self.weights)):
                    dot_value = np.dot(a[l], self.weights[l])
                    activation = self.activation(dot_value)
                    a.append(activation)
            # output layer
            error = y[i] - a[-1]
            deltas = [error * self.activation_prime(a[-1])]

            # we need to begin at the second to last layer 
            # (a layer before the output layer)
            for l in range(len(a) - 2, 0, -1): 
                deltas.append(deltas[-1].dot(self.weights[l].T)*self.activation_prime(a[l]))

            # reverse
            # [level3(output)->level2(hidden)]  => [level2(hidden)->level3(output)]
            deltas.reverse()

            # backpropagation
            # 1. Multiply its output delta and input activation 
            #    to get the gradient of the weight.
            # 2. Subtract a ratio (percentage) of the gradient from the weight.
            for i in range(len(self.weights)):
                layer = np.atleast_2d(a[i])
                delta = np.atleast_2d(deltas[i])
                self.weights[i] += learning_rate * layer.T.dot(delta)

            if k % 10000 == 0: print 'epochs:', k

    def predict(self, x): 
        a = np.concatenate((np.ones(1).T, np.array(x)), axis=1)      
        for l in range(0, len(self.weights)):
            a = self.activation(np.dot(a, self.weights[l]))
        return a

if __name__ == '__main__':

    nn = NeuralNetwork([2,2,1])
    X = np.array([[0, 0],
                  [0, 1],
                  [1, 0],
                  [1, 1]])
    y = np.array([0, 1, 1, 0])
    nn.fit(X, y)
    for e in X:
        print(e,nn.predict(e))

Output:

epochs: 0
epochs: 10000
epochs: 20000
epochs: 30000
epochs: 40000
epochs: 50000
epochs: 60000
epochs: 70000
epochs: 80000
epochs: 90000
(array([0, 0]), array([  9.14891326e-05]))
(array([0, 1]), array([ 0.99557796]))
(array([1, 0]), array([ 0.99707463]))
(array([1, 1]), array([ 0.00090973]))

1. Neural Networks in Python
2. Coursera: Machine Learning
3. wiki - Backpropagation
4. The Backpropagation Algorithm

Hello,

I'm a novice programmer in Python and new to Deep Learning. Was reading your example of the XOR with one hidden layer and backpropagation seen in:

https://www.bogotobogo.com/python/python_Neural_Networks_Backpropagation_for_XOR_using_one_hidden_layer.php

I've installed python 3.7 and the most recent version of SciPy and tried running the code provided in this example. I ran into some problems with the predict function. Running the code gave me the following error:

"File "backPropXor.py", line 78, in predict
    a = np.concatenate((np.ones(1).T, np.array(x)), axis=1)
numpy.core._internal.AxisError: axis 1 is out of bounds for array of dimension 1"

I tried rewriting the that line as following:

a = np.concatenate((np.array([[1]]), np.array([x])), axis=1)

which solved my problem. The code runs with out any errors.

Lastly I want to thank you for providing good introduction to Machine Learning.

Regards, Hreinn Juliusson

Machine Learning with scikit-learn

scikit-learn installation

scikit-learn : Features and feature extraction - iris dataset

scikit-learn : Machine Learning Quick Preview

scikit-learn : Data Preprocessing I - Missing / Categorical data

scikit-learn : Data Preprocessing II - Partitioning a dataset / Feature scaling / Feature Selection / Regularization

scikit-learn : Data Preprocessing III - Dimensionality reduction vis Sequential feature selection / Assessing feature importance via random forests

Data Compression via Dimensionality Reduction I - Principal component analysis (PCA)

scikit-learn : Data Compression via Dimensionality Reduction II - Linear Discriminant Analysis (LDA)

scikit-learn : Data Compression via Dimensionality Reduction III - Nonlinear mappings via kernel principal component (KPCA) analysis

scikit-learn : Logistic Regression, Overfitting & regularization

scikit-learn : Supervised Learning & Unsupervised Learning - e.g. Unsupervised PCA dimensionality reduction with iris dataset

scikit-learn : Unsupervised_Learning - KMeans clustering with iris dataset

scikit-learn : Linearly Separable Data - Linear Model & (Gaussian) radial basis function kernel (RBF kernel)

scikit-learn : Decision Tree Learning I - Entropy, Gini, and Information Gain

scikit-learn : Decision Tree Learning II - Constructing the Decision Tree

scikit-learn : Random Decision Forests Classification

scikit-learn : Support Vector Machines (SVM)

scikit-learn : Support Vector Machines (SVM) II

Flask with Embedded Machine Learning I : Serializing with pickle and DB setup

Flask with Embedded Machine Learning II : Basic Flask App

Flask with Embedded Machine Learning III : Embedding Classifier

Flask with Embedded Machine Learning IV : Deploy

Flask with Embedded Machine Learning V : Updating the classifier

scikit-learn : Sample of a spam comment filter using SVM - classifying a good one or a bad one

---

Machine learning algorithms and concepts

Batch gradient descent algorithm

Single Layer Neural Network - Perceptron model on the Iris dataset using Heaviside step activation function

Batch gradient descent versus stochastic gradient descent

Single Layer Neural Network - Adaptive Linear Neuron using linear (identity) activation function with batch gradient descent method

Single Layer Neural Network : Adaptive Linear Neuron using linear (identity) activation function with stochastic gradient descent (SGD)

Logistic Regression

VC (Vapnik-Chervonenkis) Dimension and Shatter

Bias-variance tradeoff

Maximum Likelihood Estimation (MLE)

Neural Networks with backpropagation for XOR using one hidden layer

minHash

tf-idf weight

Natural Language Processing (NLP): Sentiment Analysis I (IMDb & bag-of-words)

Natural Language Processing (NLP): Sentiment Analysis II (tokenization, stemming, and stop words)

Natural Language Processing (NLP): Sentiment Analysis III (training & cross validation)

Natural Language Processing (NLP): Sentiment Analysis IV (out-of-core)

Locality-Sensitive Hashing (LSH) using Cosine Distance (Cosine Similarity)

---

Artificial Neural Networks (ANN)

[Note] Sources are available at Github - Jupyter notebook files

1. Introduction

2. Forward Propagation

3. Gradient Descent

4. Backpropagation of Errors

5. Checking gradient

6. Training via BFGS

7. Overfitting & Regularization

8. Deep Learning I : Image Recognition (Image uploading)

9. Deep Learning II : Image Recognition (Image classification)

10 - Deep Learning III : Deep Learning III : Theano, TensorFlow, and Keras