Artificial Neural Network (ANN) 9 - Deep Learning II : Image Recognition (Image Classification)
Continued from Deep Learning I : Image Recognition (Image uploading).
In this section, we will now implement the code with one hidden, and one output layer to classify the MNIST images:
import numpy as np
from scipy.special import expit
import sys
class NeuralNetMLP(object):
""" Feedforward neural network / Multi-layer perceptron classifier.
Parameters
------------
n_output : int
Number of output units, should be equal to the
number of unique class labels.
n_features : int
Number of features (dimensions) in the target dataset.
Should be equal to the number of columns in the X array.
n_hidden : int (default: 30)
Number of hidden units.
l1 : float (default: 0.0)
Lambda value for L1-regularization.
No regularization if l1=0.0 (default)
l2 : float (default: 0.0)
Lambda value for L2-regularization.
No regularization if l2=0.0 (default)
epochs : int (default: 500)
Number of passes over the training set.
eta : float (default: 0.001)
Learning rate.
alpha : float (default: 0.0)
Momentum constant. Factor multiplied with the
gradient of the previous epoch t-1 to improve
learning speed
w(t) := w(t) - (grad(t) + alpha*grad(t-1))
decrease_const : float (default: 0.0)
Decrease constant. Shrinks the learning rate
after each epoch via eta / (1 + epoch*decrease_const)
shuffle : bool (default: True)
Shuffles training data every epoch if True to prevent circles.
minibatches : int (default: 1)
Divides training data into k minibatches for efficiency.
Normal gradient descent learning if k=1 (default).
random_state : int (default: None)
Set random state for shuffling and initializing the weights.
Attributes
-----------
cost_ : list
Sum of squared errors after each epoch.
"""
def __init__(self, n_output, n_features, n_hidden=30,
l1=0.0, l2=0.0, epochs=500, eta=0.001,
alpha=0.0, decrease_const=0.0, shuffle=True,
minibatches=1, random_state=None):
np.random.seed(random_state)
self.n_output = n_output
self.n_features = n_features
self.n_hidden = n_hidden
self.w1, self.w2 = self._initialize_weights()
self.l1 = l1
self.l2 = l2
self.epochs = epochs
self.eta = eta
self.alpha = alpha
self.decrease_const = decrease_const
self.shuffle = shuffle
self.minibatches = minibatches
def _encode_labels(self, y, k):
"""Encode labels into one-hot representation
Parameters
------------
y : array, shape = [n_samples]
Target values.
Returns
-----------
onehot : array, shape = (n_labels, n_samples)
"""
onehot = np.zeros((k, y.shape[0]))
for idx, val in enumerate(y):
onehot[val, idx] = 1.0
return onehot
def _initialize_weights(self):
"""Initialize weights with small random numbers."""
w1 = np.random.uniform(-1.0, 1.0,
size=self.n_hidden*(self.n_features + 1))
w1 = w1.reshape(self.n_hidden, self.n_features + 1)
w2 = np.random.uniform(-1.0, 1.0,
size=self.n_output*(self.n_hidden + 1))
w2 = w2.reshape(self.n_output, self.n_hidden + 1)
return w1, w2
def _sigmoid(self, z):
"""Compute logistic function (sigmoid)
Uses scipy.special.expit to avoid overflow
error for very small input values z.
"""
# return 1.0 / (1.0 + np.exp(-z))
return expit(z)
def _sigmoid_gradient(self, z):
"""Compute gradient of the logistic function"""
sg = self._sigmoid(z)
return sg * (1.0 - sg)
def _add_bias_unit(self, X, how='column'):
"""Add bias unit (column or row of 1s) to array at index 0"""
if how == 'column':
X_new = np.ones((X.shape[0], X.shape[1] + 1))
X_new[:, 1:] = X
elif how == 'row':
X_new = np.ones((X.shape[0] + 1, X.shape[1]))
X_new[1:, :] = X
else:
raise AttributeError('`how` must be `column` or `row`')
return X_new
def _feedforward(self, X, w1, w2):
"""Compute feedforward step
Parameters
-----------
X : array, shape = [n_samples, n_features]
Input layer with original features.
w1 : array, shape = [n_hidden_units, n_features]
Weight matrix for input layer -> hidden layer.
w2 : array, shape = [n_output_units, n_hidden_units]
Weight matrix for hidden layer -> output layer.
Returns
----------
a1 : array, shape = [n_samples, n_features+1]
Input values with bias unit.
z2 : array, shape = [n_hidden, n_samples]
Net input of hidden layer.
a2 : array, shape = [n_hidden+1, n_samples]
Activation of hidden layer.
z3 : array, shape = [n_output_units, n_samples]
Net input of output layer.
a3 : array, shape = [n_output_units, n_samples]
Activation of output layer.
"""
a1 = self._add_bias_unit(X, how='column')
z2 = w1.dot(a1.T)
a2 = self._sigmoid(z2)
a2 = self._add_bias_unit(a2, how='row')
z3 = w2.dot(a2)
a3 = self._sigmoid(z3)
return a1, z2, a2, z3, a3
def _L2_reg(self, lambda_, w1, w2):
"""Compute L2-regularization cost"""
return (lambda_/2.0) * (np.sum(w1[:, 1:] ** 2) +
np.sum(w2[:, 1:] ** 2))
def _L1_reg(self, lambda_, w1, w2):
"""Compute L1-regularization cost"""
return (lambda_/2.0) * (np.abs(w1[:, 1:]).sum() +
np.abs(w2[:, 1:]).sum())
def _get_cost(self, y_enc, output, w1, w2):
"""Compute cost function.
Parameters
----------
y_enc : array, shape = (n_labels, n_samples)
one-hot encoded class labels.
output : array, shape = [n_output_units, n_samples]
Activation of the output layer (feedforward)
w1 : array, shape = [n_hidden_units, n_features]
Weight matrix for input layer -> hidden layer.
w2 : array, shape = [n_output_units, n_hidden_units]
Weight matrix for hidden layer -> output layer.
Returns
---------
cost : float
Regularized cost.
"""
term1 = -y_enc * (np.log(output))
term2 = (1.0 - y_enc) * np.log(1.0 - output)
cost = np.sum(term1 - term2)
L1_term = self._L1_reg(self.l1, w1, w2)
L2_term = self._L2_reg(self.l2, w1, w2)
cost = cost + L1_term + L2_term
return cost
def _get_gradient(self, a1, a2, a3, z2, y_enc, w1, w2):
""" Compute gradient step using backpropagation.
Parameters
------------
a1 : array, shape = [n_samples, n_features+1]
Input values with bias unit.
a2 : array, shape = [n_hidden+1, n_samples]
Activation of hidden layer.
a3 : array, shape = [n_output_units, n_samples]
Activation of output layer.
z2 : array, shape = [n_hidden, n_samples]
Net input of hidden layer.
y_enc : array, shape = (n_labels, n_samples)
one-hot encoded class labels.
w1 : array, shape = [n_hidden_units, n_features]
Weight matrix for input layer -> hidden layer.
w2 : array, shape = [n_output_units, n_hidden_units]
Weight matrix for hidden layer -> output layer.
Returns
---------
grad1 : array, shape = [n_hidden_units, n_features]
Gradient of the weight matrix w1.
grad2 : array, shape = [n_output_units, n_hidden_units]
Gradient of the weight matrix w2.
"""
# backpropagation
sigma3 = a3 - y_enc
z2 = self._add_bias_unit(z2, how='row')
sigma2 = w2.T.dot(sigma3) * self._sigmoid_gradient(z2)
sigma2 = sigma2[1:, :]
grad1 = sigma2.dot(a1)
grad2 = sigma3.dot(a2.T)
# regularize
grad1[:, 1:] += self.l2 * w1[:, 1:]
grad1[:, 1:] += self.l1 * np.sign(w1[:, 1:])
grad2[:, 1:] += self.l2 * w2[:, 1:]
grad2[:, 1:] += self.l1 * np.sign(w2[:, 1:])
return grad1, grad2
def predict(self, X):
"""Predict class labels
Parameters
-----------
X : array, shape = [n_samples, n_features]
Input layer with original features.
Returns:
----------
y_pred : array, shape = [n_samples]
Predicted class labels.
"""
if len(X.shape) != 2:
raise AttributeError('X must be a [n_samples, n_features] array.\n'
'Use X[:,None] for 1-feature classification,'
'\nor X[[i]] for 1-sample classification')
a1, z2, a2, z3, a3 = self._feedforward(X, self.w1, self.w2)
y_pred = np.argmax(z3, axis=0)
return y_pred
def fit(self, X, y, print_progress=False):
""" Learn weights from training data.
Parameters
-----------
X : array, shape = [n_samples, n_features]
Input layer with original features.
y : array, shape = [n_samples]
Target class labels.
print_progress : bool (default: False)
Prints progress as the number of epochs
to stderr.
Returns:
----------
self
"""
self.cost_ = []
X_data, y_data = X.copy(), y.copy()
y_enc = self._encode_labels(y, self.n_output)
delta_w1_prev = np.zeros(self.w1.shape)
delta_w2_prev = np.zeros(self.w2.shape)
for i in range(self.epochs):
# adaptive learning rate
self.eta /= (1 + self.decrease_const*i)
if print_progress:
sys.stderr.write('\rEpoch: %d/%d' % (i+1, self.epochs))
sys.stderr.flush()
if self.shuffle:
idx = np.random.permutation(y_data.shape[0])
X_data, y_enc = X_data[idx], y_enc[:, idx]
mini = np.array_split(range(y_data.shape[0]), self.minibatches)
for idx in mini:
# feedforward
a1, z2, a2, z3, a3 = self._feedforward(X_data[idx],
self.w1,
self.w2)
cost = self._get_cost(y_enc=y_enc[:, idx],
output=a3,
w1=self.w1,
w2=self.w2)
self.cost_.append(cost)
# compute gradient via backpropagation
grad1, grad2 = self._get_gradient(a1=a1, a2=a2,
a3=a3, z2=z2,
y_enc=y_enc[:, idx],
w1=self.w1,
w2=self.w2)
delta_w1, delta_w2 = self.eta * grad1, self.eta * grad2
self.w1 -= (delta_w1 + (self.alpha * delta_w1_prev))
self.w2 -= (delta_w2 + (self.alpha * delta_w2_prev))
delta_w1_prev, delta_w2_prev = delta_w1, delta_w2
return self
Here is the summary of the parameters used in the code:
- l2 : The $\lambda$ parameter for L2 regularization to decrease the degree of overfitting; equivalently, $l1$ is the $\lambda$ parameter for L1 regularization.
- epochs : The number of passes over the training set. eta : The learning rate $\eta$.
- alpha : A parameter for momentum learning to add a factor of the previous gradient to the weight update for faster learning $\Delta \mathbf w_t = \eta \nabla J (\mathbf w_t) + \alpha \Delta \mathbf w_{t-1}$ (where $t$ is the current time step or epoch).
- decrease_const : The decrease constant $d$ for an adaptive learning rate $\eta$ that decreases over time for better convergence $\frac{\eta}{1 + t \times d}$.
- shuffle : Shuffling the training set prior to every epoch to prevent the algorithm from getting stuck in cycles.
- Minibatches : Splitting of the training data into SkS mini-batches in each epoch. The gradient is computed for each mini-batch separately instead of the entire training data for faster learning.
Let's initialize our neural network with 784 input units (n_features), 50 hidden units (n_hidden), and 10 output units (n_output):
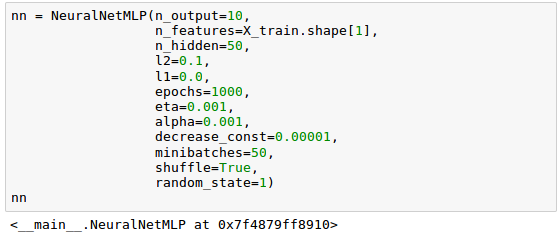
Now it's time to train our neural network using 60,000 samples from the already shuffled MNIST training dataset. It may take a while:

We can now visualize the convergence of the cost function which is saved in a cost_ list. Note that we only plot every 50th step since we used the parameter minibatches=50, 50 mini-batches x 1000 epochs.
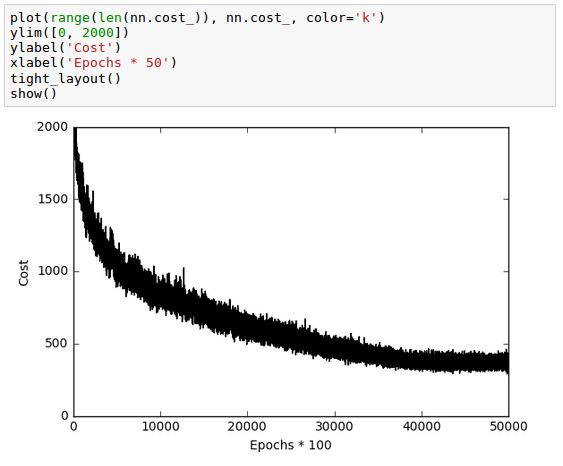
As we see in the plot above, while though the optimization algorithm converged around 800 epochs (40,000/50 = 800), the graph of the cost function looks very noisy. That's because we trained our neural network with mini-batch learning which computes the gradient using batch of 50 samples from dataset rather one sample at a time.
Note that the stochastic gradient descent (SGD) computes the gradient using a single sample while most applications of SGD actually use a minibatch of several samples.
We can make the noisy plot smoother by averaging over the mini-batch intervals:
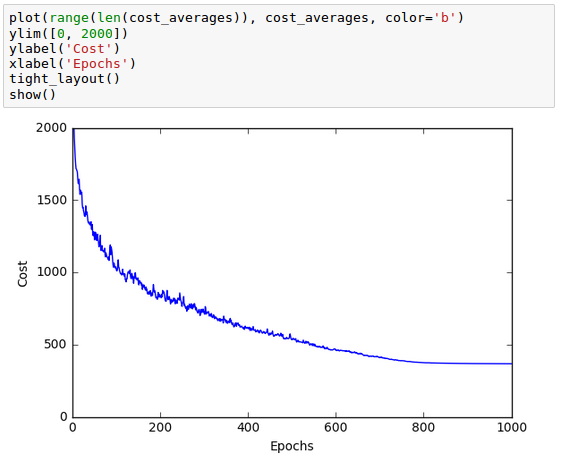
We can evaluate the performance of the model by calculating the prediction accuracy:

Though we can see the model classifies most of the training digits correctly, let's see how does the model perform on the 10,000 test images:

Considering the small discrepancy between the two outputs, training and test dataset, we can see our model performs pretty well.
In order to further fine-tune our model, we may want to tweak the followings:
- the number of hidden units
- values of the regularization parameters
- learning rate
- the values of the decrease constant.
To make our model better, we need to know what image samples our model struggles with. Here are the samples that our model misclassified:
The picture below is the samples (6 x 5) that our model misclassifed. The 't' stands for the true class label while 'p' stands for the predicted class label:
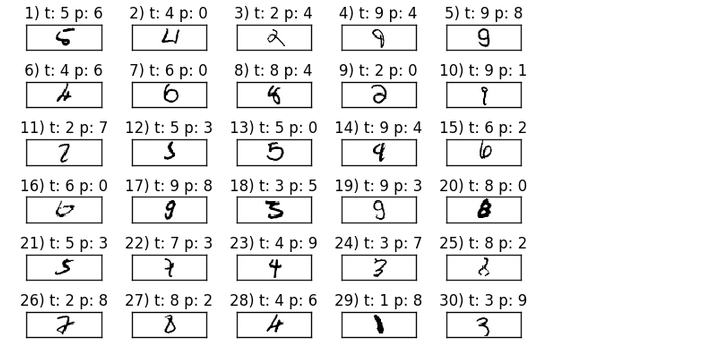
Considering some of those images are even challenging for us humans to classify correctly, our model did perform relatively well!
Python Machine Learning by Sebastian Raschka
part8-9-ImageRecognition.ipynb
10 - Deep Learning III : Deep Learning III : Theano, TensorFlow, and Keras
Machine Learning with scikit-learn
scikit-learn installation
scikit-learn : Features and feature extraction - iris dataset
scikit-learn : Machine Learning Quick Preview
scikit-learn : Data Preprocessing I - Missing / Categorical data
scikit-learn : Data Preprocessing II - Partitioning a dataset / Feature scaling / Feature Selection / Regularization
scikit-learn : Data Preprocessing III - Dimensionality reduction vis Sequential feature selection / Assessing feature importance via random forests
Data Compression via Dimensionality Reduction I - Principal component analysis (PCA)
scikit-learn : Data Compression via Dimensionality Reduction II - Linear Discriminant Analysis (LDA)
scikit-learn : Data Compression via Dimensionality Reduction III - Nonlinear mappings via kernel principal component (KPCA) analysis
scikit-learn : Logistic Regression, Overfitting & regularization
scikit-learn : Supervised Learning & Unsupervised Learning - e.g. Unsupervised PCA dimensionality reduction with iris dataset
scikit-learn : Unsupervised_Learning - KMeans clustering with iris dataset
scikit-learn : Linearly Separable Data - Linear Model & (Gaussian) radial basis function kernel (RBF kernel)
scikit-learn : Decision Tree Learning I - Entropy, Gini, and Information Gain
scikit-learn : Decision Tree Learning II - Constructing the Decision Tree
scikit-learn : Random Decision Forests Classification
scikit-learn : Support Vector Machines (SVM)
scikit-learn : Support Vector Machines (SVM) II
Flask with Embedded Machine Learning I : Serializing with pickle and DB setup
Flask with Embedded Machine Learning II : Basic Flask App
Flask with Embedded Machine Learning III : Embedding Classifier
Flask with Embedded Machine Learning IV : Deploy
Flask with Embedded Machine Learning V : Updating the classifier
scikit-learn : Sample of a spam comment filter using SVM - classifying a good one or a bad one
Machine learning algorithms and concepts
Batch gradient descent algorithmSingle Layer Neural Network - Perceptron model on the Iris dataset using Heaviside step activation function
Batch gradient descent versus stochastic gradient descent
Single Layer Neural Network - Adaptive Linear Neuron using linear (identity) activation function with batch gradient descent method
Single Layer Neural Network : Adaptive Linear Neuron using linear (identity) activation function with stochastic gradient descent (SGD)
Logistic Regression
VC (Vapnik-Chervonenkis) Dimension and Shatter
Bias-variance tradeoff
Maximum Likelihood Estimation (MLE)
Neural Networks with backpropagation for XOR using one hidden layer
minHash
tf-idf weight
Natural Language Processing (NLP): Sentiment Analysis I (IMDb & bag-of-words)
Natural Language Processing (NLP): Sentiment Analysis II (tokenization, stemming, and stop words)
Natural Language Processing (NLP): Sentiment Analysis III (training & cross validation)
Natural Language Processing (NLP): Sentiment Analysis IV (out-of-core)
Locality-Sensitive Hashing (LSH) using Cosine Distance (Cosine Similarity)
Artificial Neural Networks (ANN)
[Note] Sources are available at Github - Jupyter notebook files1. Introduction
2. Forward Propagation
3. Gradient Descent
4. Backpropagation of Errors
5. Checking gradient
6. Training via BFGS
7. Overfitting & Regularization
8. Deep Learning I : Image Recognition (Image uploading)
9. Deep Learning II : Image Recognition (Image classification)
10 - Deep Learning III : Deep Learning III : Theano, TensorFlow, and Keras
Ph.D. / Golden Gate Ave, San Francisco / Seoul National Univ / Carnegie Mellon / UC Berkeley / DevOps / Deep Learning / Visualization