Maximum Likelihood Estimation (MLE)

bogotobogo.com site search:

Introduction

Wiki describes Maximum Likelihood Estimation (MLE) like this:

In statistics, maximum likelihood estimation (MLE) is a method of estimating the parameters of a statistical model given data.

We'll start with a binomial distribution.

Suppose we have dataset : 0,1,1,0,1,1 with the probability like this:

$$ p(x=1)=\mu, \quad p(x=0)=1-\mu$$

What is the maximum likelihood of the parameter $\mu$?

We can think of the dataset as the outcome of coin toss, and 1 for head, 0 for tail. So, the coin appears biased towards heads. But how much?

Let's multiply the probability of each data point as a function of the parameter $\mu$:

$$ L(\mu) = p(0)p(1)p(1)p(0)p(1)p(1) = (1-\mu)\mu\mu(1-\mu)\mu\mu = (1-\mu)^2\mu^4$$

Then, log of $L(\mu)$ becomes:

$$ log(L(\mu))=2log(1-\mu)+4log\mu$$

To get the value of $\mu$ which makes $L(\mu)$ max, let's get the derivative of $log(L(\mu))$:

$$ (logL)^\prime = \frac {-2}{1-\mu} + \frac{4}{\mu} = 0$$

This gives us $\mu = 2/3$.

Still, we're not sure it's just a saddle or a real max. So, let's get a \mu which makes 2nd derivative equals to 0:

$$ (logL)^{\prime \prime} = \frac {2}{(1-\mu)^2}- \frac {4}{\mu^2} $$

We get negative value if we put $\mu = 2/3$ in the 2nd derivative. So, we can be sure it's max when $\mu = 2/3$.

So, if the dataset is for coin toss, then we can say the coin's bias($\mu$) for head is 2/3!

The sample we used just has one parameter ($\mu$: bias towards heads).

In the next section, we'll deal with more general case where we want to estimate multiple parameters.

bogotobogo.com site search:

Maximum likelihood estimation (MLE)

Let's start by looking into the following maximum likelihood function:

$$ L(w)=\prod_i^n(\phi(z^{(i)})^{y^{(i)}}(1-\phi(z^{(i)}))^{1-y^{(i)}}$$

Note that compared with the $L(\mu)$ in the previous section, here $\phi(z)$ is the (conditional) probability.

$$ \phi(z)=p(y=1|x;w)=\frac{1}{1+e^{-z}}$$

where $z$ is the net input:

$$ z = \sum_iw_ix_i$$

We learned that we can use the logistic regression model to predict probabilities and class labels.

Now let's think about the parameters of the model, for example, weights $w$ with the likelihood $L(w)$ defined above. We want to maximize it when we build a logistic regression model.

In other words, maximizing the likelihood means maximizing the probability. Since we are talking about "cost", lets reverse the likelihood function so that we can minimize a cost function $J$.

For convenience (in case when we use gradient or stochastic gradient descent), we may want to use log-likelihood function as our "cost function", $J(w)$, that can be minimized using gradient descent:

$$ log(L(w))=\sum_i^n y^{(i)}log(\phi(z^{(i)})+(1-y^{(i)})log(1-\phi(z^{(i)}))$$ $$ J(w) = \sum_i^n -y^{(i)}log(\phi(z^{(i)})-(1-y^{(i)})log(1-\phi(z^{(i)}))$$

To make the property of this cost function more clear, let's take a look at the cost function with just one single-sample instance:

$$ J(\phi(z),y;w)=\sum_i^n -\; y log\phi(z)-(1-y) \; log(1-\phi(z)) $$

If we look at the equation carefully, we can see that the first term becomes zero if $y = 0$, while the second term becomes zero if $y = 1$, respectively as shown in the picture below:

$$ J(\phi(z),y;w)= \begin{cases}-log(\phi(z)) & if \; y=1 \\ -log(1-\phi(z)) & if \; y=0 \end{cases}$$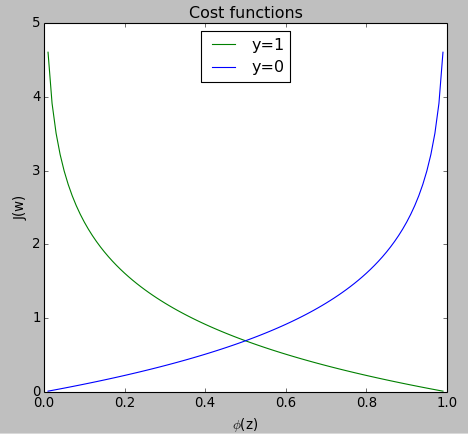

As we can see from the picture, the cost approaches 0 (green) if we correctly predict that a sample belongs to class 1. Similarly, we can see on the y axis that the cost also approaches 0 if we correctly predict y = 0 (blue).

However, if the prediction is wrong, we penalize wrong predictions by increasing the cost to large a value.

Picture code:

import matplotlib.pyplot as plt
import numpy as np

phi = np.arange(0.01, 1.0, 0.01)
j1 = -np.log(phi)
j0 = -np.log(1-phi)
plt.plot(phi, j1, color="green", label="y=1")
plt.plot(phi, j0, color="blue", label="y=0")

plt.xlabel('$\phi$(z)')
plt.ylabel('J(w)')
plt.title('Cost functions')
plt.grid(False)
plt.legend(loc='upper center')
plt.show()

We can use Jupyter as well via inline matplotlib feature: