Bayes Rule
Q: Approximately 1% of women aged 40-50 have breast cancer.
A woman with breast cancer has a 90% chance of a positive test from a mammogram,
while a woman without has a 10% chance of a false positive result.
What is the probability a woman has breast cancer given that she just had a positive test?
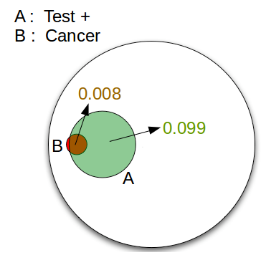
Let $A$ = "a positive test" and $B$ = "the woman has breast cancer". We wish to calculate a woman has breast cancer(B) given that she just had a positive test (A), B for given A, $P(B|A)$.

$$P(B|A) = \frac{P(A \cap B)}{P(A \cap B) + P(A \cap B^c)}$$
Using multiplication rule:
$$P(A \cap B) = P(B)P(A|B) = 0.01 \times 0.8 = 0.008$$ $$P(A \cap B^C) = P(B^C)P(A|B^C) = 0.99 \times 0.1 = 0.099$$So, we get:
$$P(B|A) = \frac{0.008}{0.008 + 0.099} = 0.0747$$About a 7.5% chance of actually having breast cancer given a positive mammogram!
May be too simple:
def Bayes(prior, conditional): A_cap_B, A_cap_Bc = [conditional[i]*prior[i] for i in range(len(prior))] posterior = A_cap_B /(A_cap_B + A_cap_Bc) return posterior prior = [0.01, 0.99] # Probability A, Ac conditional = [0.8, 0.1] # Probability A, Ac for given B # returns probability of B for given A print Bayes(prior, conditional)
Output:
0.0747663551402
Ph.D. / Golden Gate Ave, San Francisco / Seoul National Univ / Carnegie Mellon / UC Berkeley / DevOps / Deep Learning / Visualization