Algorithms - Radix Sort
We may say a radix is a position in a number.
In the decimal system, a radix is just a digit in a decimal number. For example, the number 42 has two digits, or two radices, which are 4 and 2. In hexadecimal, the radix is 8 bits wide. For example, the hexadecimal number 0xAB has two radices, A and B. The Radix Sort gets its name from those radices, because the method first sorts the input values according to their first radix, then according to the second one, and so on. The Radix Sort is then a multipass sort, and the number of passes equals the number of radices in the input values.
- Least significant digit (LSD)
Short keys come before longer keys, and keys of the same length are sorted lexicographically.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10 - Most significant digit (MSD)
MSD radix sorts use lexicographic order, which is suitable for sorting strings, such as words, or fixed-length integer representations.
"b, c, d, e, f, g, h, i, j, ba" would be lexicographically sorted as "b, ba, c, d, e, f, g, h, i, j"
Numbers from 1 to 10 would be output as 1, 10, 2, 3, 4, 5, 6, 7, 8, 9
Each key is first figuratively dropped into one level of buckets corresponding to the value of the rightmost digit. Each bucket preserves the original order of the keys as the keys are dropped into. There is a one-to-one correspondence between the number of buckets and the number of values that can be represented by a digit. Then, the process repeats with the next neighboring digit until there are no more digits to process. In other words:
- Take the least significant digit (or group of bits, both being examples of radices) of each key.
- Group the keys based on that digit, but otherwise keep the original order of keys. (This is what makes the LSD radix sort a stable sort).
- Repeat the grouping process with each more significant digit.
The sort in step 2 is usually done using bucket sort or counting sort, which are efficient in this case since there are usually only a small number of digits.
-from wiki
C++ Code:
#include <iostream>
using namespace std;
const int MAX = 10;
void print(int *a,int sz) {
for(int i = 0; i < sz; i++)
cout << a[i] << " ";
cout << endl;
}
void RadixSortLSD(int *a, int arraySize)
{
int i, bucket[MAX], maxVal = 0, digitPosition =1 ;
for(i = 0; i < arraySize; i++) {
if(a[i] > maxVal) maxVal = a[i];
}
int pass = 1; // used to show the progress
/* maxVal: this variable decide the while-loop count
if maxVal is 3 digits, then we loop through 3 times */
while(maxVal/digitPosition > 0) {
/* reset counter */
int digitCount[10] = {0};
/* count pos-th digits (keys) */
for(i = 0; i < arraySize; i++)
digitCount[a[i]/digitPosition%10]++;
/* accumulated count */
for(i = 1; i < 10; i++)
digitCount[i] += digitCount[i-1];
/* To keep the order, start from back side */
for(i = arraySize - 1; i >= 0; i--)
bucket[--digitCount[a[i]/digitPosition%10]] = a[i];
/* rearrange the original array using elements in the bucket */
for(i = 0; i < arraySize; i++)
a[i] = bucket[i];
/* at this point, a array is sorted by digitPosition-th digit */
cout << "pass #" << pass++ << ": ";
print(a,arraySize);
/* move up the digit position */
digitPosition *= 10;
}
}
int main()
{
int a[] = {170, 45, 75, 90, 2, 24, 802, 66};
const size_t sz = sizeof(a)/sizeof(a[0]);
cout << "pass #0: ";
print(a,sz);
RadixSortLSD(&a;[0],sz);
return 0;
}
Output from the run is:
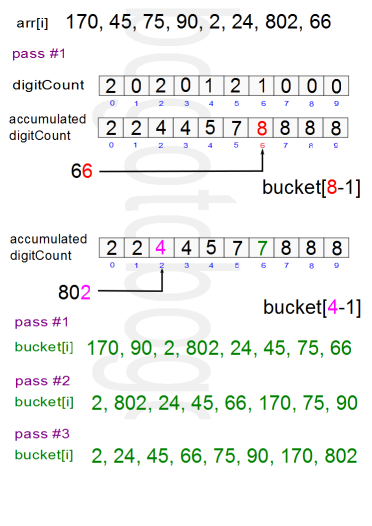
pass #0: 170 45 75 90 2 24 802 66 pass #1: 170 90 2 802 24 45 75 66 pass #2: 2 802 24 45 66 170 75 90 pass #3: 2 24 45 66 75 90 170 802
Here is a diagram for the first pass of the code above.
Ph.D. / Golden Gate Ave, San Francisco / Seoul National Univ / Carnegie Mellon / UC Berkeley / DevOps / Deep Learning / Visualization