Algorithms - Knapsack
A thief robbing a store finds n items. The ith item is worth v[i] dollars and weighs w[i] pounds, where v[i] and w[i] are integers. The thief wants to take as valuable a load as possible, but he can carry at most W pounds in his knapsack, for some integer W.
Which items should he take? (We call this the 0-1 knapsack problem because for each item, the thief must either take it or leave it behind, he cannot take a fractional amount of an item or take an item more than once.) - from Introduction to Algorithms, 3rd Ed. by Thomas H. Cormen et al.
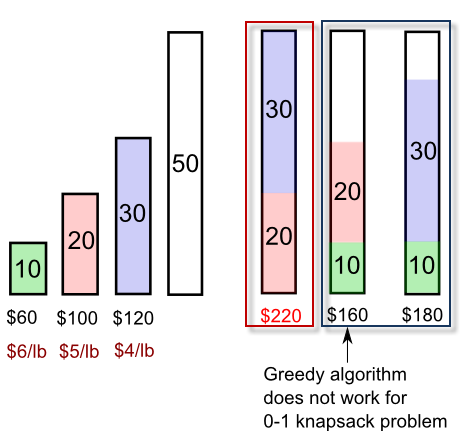
The thief must choose a subset of three items (green, pink, or blue) shown in the picture above. The total weight should not exceed 50 pounds. The optimal solution is selecting item #2 (pink) and item #3 (blue). Any selection of the item #1 (greedy algorithm) which has the greatest value per pound ($6/lb) does not produce optimal solutions as shown in 2nd and 3rd knapsacks. However, if it's not a problem of 0-1 knapsack by allowing fractional can give us the the best result with item #1: (item#1 + item#2 + 2/3*item#3) = (10 + 20 + 2/3*(30)) pounds = 50 pounds => $60 + $100 + 2/3*($120) = $240 > $220.
#include <iostream>
using namespace std;
int MAX(int a, int b) { return (a > b) ? a : b ; }
int knapsack(int W, int weight[], int value[], int n)
{
//base case
if(n == 0 || weight <= 0) return 0;
// any time can't be w > W, and it shouldn't be included
if(weight[n-1] > W) return knapsack(W, weight, value, n-1);
/* return max between the cases
(a) n-th item included and (b) n-th item NOT included */
return MAX( value[n-1] + knapsack(W-weight[n-1], weight, value, n-1),
knapsack(W, weight, value, n-1) );
}
int main()
{
int weight[] = {10, 20, 30};
int value[] = {60, 100, 120};
int wLimit = 50;
cout << knapsack(wLimit, weight, value, 3) << endl; // $220
return 0;
}
#include <iostream>
#include <vector>
using namespace std;
int MAX(int a, int b) { return (a > b) ? a : b ; }
int knapsack(int W, int weight[], int value[], int n, int s[])
{
/* m[i][w] to be the maximum value that can be attained
with weight less than or equal to w using items up to i*/
vector<vector<int> > m(n+1, vector<int>(W+1, 0)); // m[n+1][W+1]
for(int jw = 0; jw <= W; jw++) m[0][jw] = 0;
for(int i = 1; i <=n; i++) {
for(int jw = 0; jw <= W; jw++) {
// A case when the new item is more than the current weight limit
if(weight[i-1] > jw)
m[i][jw] = m[i-1][jw];
// A case for weight[i] < jw
else {
m[i][jw] = MAX( m[i-1][jw], value[i-1] + m[i-1][jw-weight[i-1]] );
s[jw] = i;
}
}
}
return m[n][W];
}
int main()
{
int weight[] = {10, 20, 30};
int value[] = {60, 100, 120};
int wLimit = 50;
int *s = new int[51];
cout << "Max value: ";
cout << knapsack(wLimit, weight, value, 3, s) << endl; // $220
int k = wLimit;
cout << "weight used: " ;
while(k) {
cout << weight[s[k]-1] << " ";
k = k - weight[s[k]-1];
}
return 0;
}
Output:
Max value: 220 weight used: 30 20
For other dynamic programming samples, please visit Dynamic Programming.
Ph.D. / Golden Gate Ave, San Francisco / Seoul National Univ / Carnegie Mellon / UC Berkeley / DevOps / Deep Learning / Visualization