Algorithms - Dijkstra's Shortest Path
bogotobogo.com site search:
bogotobogo.com site search:
Dijkstra's Shortest Path
Algorithm
- Mark all nodes tentative:
Set distances from source to 0 for source, and infinity for all other nodes - Loop:
Extract node N which is a node with lowest distance
Add link to N to the shortest path tree
Relax the distances of neighbors of N by lowering any better distances
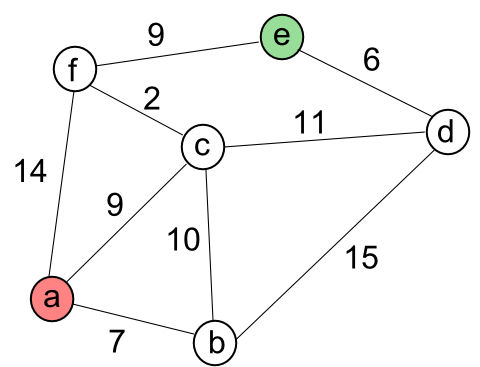
Example
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
typedef struct node_t node_t;
typedef struct edge_t edge_t;
struct edge_t {
node_t *nd; /* target of this edge */
edge_t *sibling;/* for singly linked list */
int len; /* edge cost */
};
struct node_t {
edge_t *edge; /* singly linked list of edges */
node_t *via; /* where previous node is in shortest path */
double dist; /* distance from the source */
char name[8]; /* vertex name */
int heap_idx; /* link to heap position for updating distance */
};
/*edge*/
#define BLOCK_SIZE 15
edge_t *edge_root = 0, *e_next = 0;
void add_edge(node_t *a, node_t *b, double d)
{
if (e_next == edge_root) {
edge_root = (edge_t*)malloc(sizeof(edge_t) * (BLOCK_SIZE + 1));
edge_root[BLOCK_SIZE].sibling = e_next;
e_next = edge_root + BLOCK_SIZE;
}
--e_next;
e_next->nd = b;
e_next->len = d;
e_next->sibling = a->edge;
a->edge = e_next;
}
void free_edges()
{
for (; edge_root; edge_root = e_next) {
e_next = edge_root[BLOCK_SIZE].sibling;
free(edge_root);
}
}
/* priority queue */
node_t **heap;
int heap_len;
void set_dist(node_t *nd, node_t *via, double d)
{
int i, j;
/* already knew better path */
if (nd->via && d >= nd->dist) return;
/* find existing heap entry, or create a new one */
nd->dist = d;
nd->via = via;
i = nd->heap_idx;
if (!i) i = ++heap_len;
/* upheap */
for (; i > 1 && nd->dist < heap[j = i/2]->dist; i = j)
(heap[i] = heap[j])->heap_idx = i;
heap[i] = nd;
nd->heap_idx = i;
}
node_t * pop_queue()
{
node_t *nd, *tmp;
int i, j;
if (!heap_len) return 0;
/* remove leading element, pull tail element there and downheap */
nd = heap[1];
tmp = heap[heap_len--];
for (i = 1; i < heap_len && (j = i * 2) <= heap_len; i = j) {
if (j < heap_len && heap[j]->dist > heap[j+1]->dist) j++;
if (heap[j]->dist >= tmp->dist) break;
(heap[i] = heap[j])->heap_idx = i;
}
heap[i] = tmp;
tmp->heap_idx = i;
return nd;
}
/* Dijkstra's algorithm; unreachable nodes will never make into the queue */
void calc_all(node_t *start)
{
node_t *lead;
edge_t *e;
set_dist(start, start, 0);
while ((lead = pop_queue()))
for (e = lead->edge; e; e = e->sibling)
set_dist(e->nd, lead, lead->dist + e->len);
}
void show_path(node_t *nd)
{
if (nd->via == nd)
printf("%s", nd->name);
else if (!nd->via)
printf("%s(unreached)", nd->name);
else {
show_path(nd->via);
printf("-> %s(%g) ", nd->name, nd->dist);
}
}
int main(void)
{
#define N_NODES 6
node_t *nodes = (node_t*)calloc(sizeof(node_t), N_NODES);
for (int i = 0; i < N_NODES; i++)
sprintf(nodes[i].name, "%c", 'a' + i);
add_edge(nodes, nodes+1, 7); //a-b
add_edge(nodes, nodes+2, 9); //a-c
add_edge(nodes, nodes+5, 14); //a-f
add_edge(nodes+1, nodes+2, 10); //b-c
add_edge(nodes+1, nodes+3, 15); //b-d
add_edge(nodes+2, nodes+3, 11); //c-d
add_edge(nodes+2, nodes+5, 2); //c-f
add_edge(nodes+3, nodes+4, 6); //d-e
add_edge(nodes+4, nodes+5, 9); //e-f
heap = (node_t**)calloc(sizeof(node_t), N_NODES + 1);
heap_len = 0;
calc_all(nodes);
for (int i = 0; i < N_NODES; i++) {
show_path(nodes + i);
putchar('\n');
}
//free memories
free_edges();
free(heap);
free(nodes);
return 0;
}
Output:
a a-> b(7) a-> c(9) a-> c(9) -> d(20) a-> c(9) -> d(20) -> e(26) a-> c(9) -> f(11)
Characteristics
- Finds shortest paths in increasing distance from source:
What Dijkstra's Shortest Path is really doing is leveraging this property of optimizing. Sub paths are also shortest paths, so we can build up from small paths to large paths and they all overlap. And that's why it works to go out at increasing distance and then insures that once we've gone out to a certain distance, we'll never change our path later. - Runtime depending on the efficiency of extracting minimum cost node:
We can use different data structure depending on whether edges are dense or sparse. However, in any case, the running time is superlinear linear in the size of the network, which means as the network grows larger the run time of the algorithm is going to go even more quickly and eventually if the very large network the run time would become very large. - It gives complete source/sink tree but it requires complete topology of the network.
(There is another algorithm that requires only the neighboring nodes not the whole topology:
Distance vector algorithms (wiki) which is based on Bellman Ford shortest path algorithm).
Dijkstra - Python implementation
Python implementation for the Dijkstra's Shortest Path : Dijkstra's shortest path algorithm.
Ph.D. / Golden Gate Ave, San Francisco / Seoul National Univ / Carnegie Mellon / UC Berkeley / DevOps / Deep Learning / Visualization