Algorithms - Compression: Huffman Encoding
We usually use 1 byte (8 bits) to store a character. Actually, we do not have to use all 8 bits if we have a convention for bit pattern on how to represent a specific character. Huffman encoding is doing it using greedy algorithm.
In other word, it is not always using 8 bits. Instead, depending on the frequency, we can use 3 bits, 4 bits, or 8 bits etc. By using a table giving how often each character occurs to build an optimal way of representing each character as a binary string. In that way, we can save space of storing text. Compression!
Huffman codes compress data effectively, and it typically saves 20% to 90% depending on the data being compressed.
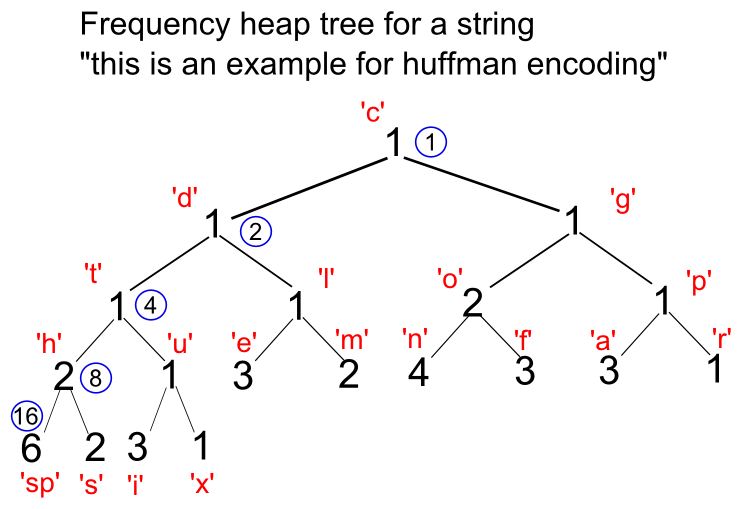
The picture below shows initial heap-tree diagram. It has the information on the frequency for each character as well as the node numbers.
#include <stdio.h>
#include <string.h>
typedef struct node_t {
struct node_t *left, *right;
int freq;
char c;
} *node;
struct node_t pool[256] = {{0}};
node qqq[255], *q = qqq - 1;
int n_nodes = 0, qend = 1;
char *code[128] = {0}, buf[1024];
node new_node(int freq, char c, node a, node b)
{
node n = pool + n_nodes++;
if (freq) n->c = c, n->freq = freq;
else {
n->left = a, n->right = b;
n->freq = a->freq + b->freq;
}
return n;
}
/* priority queue */
void qinsert(node n)
{
/* higher freq has lower priority
move up lower freq */
int j, i = qend++;
while ((j = i / 2)) {
/* compare freq of the new node with the parent's freq */
if (q[j]->freq <= n->freq) break;
q[i] = q[j], i = j;
}
q[i] = n;
}
/* remove the top element(q[1]),
and moving up other elements */
node qremove()
{
int i, l;
node n = q[i = 1];
if (qend < 2) return 0;
qend--;
while ((l = i * 2) < qend) {
if (l + 1 < qend && q[l + 1]->freq < q[l]->freq) l++;
q[i] = q[l], i = l;
}
q[i] = q[qend];
return n;
}
/* walk the tree and put 0s and 1s */
void build_code(node n, char *s, int len)
{
static char *out = buf;
if (n->c) {
s[len] = 0;
strcpy(out, s);
code[n->c] = out;
out += len + 1;
return;
}
s[len] = '0'; build_code(n->left, s, len + 1);
s[len] = '1'; build_code(n->right, s, len + 1);
}
void init(const char *s)
{
int i, freq[128] = {0};
char c[16];
/* count frequency for each character */
while (*s) freq[(int)*s++]++;
/* initial heap tree */
for (i = 0; i < 128; i++) {
if (freq[i]) qinsert(new_node(freq[i], i, 0, 0));
}
/* complete heap while merging node staring from the lower frequency nodes */
/* This is done in the following steps
(1) remove top two nodes which have the highest priority (lowest freq)
(2) make a new one with the two removed nodes while adding the two freqs
(3) when we make the new node, it remembers its children as left/right nodes
(4) keep merging the nodes until there is only one node left
*/
while (qend > 2) {
qinsert(new_node(0, 0, qremove(), qremove()));
}
/* (1) Traverse the constructed tree from root to leaves
(2) Assign and accumulate
a '0' for left branch and a '1' for the right branch at each node.
(3) The accumulated zeros and ones at each leaf constitute a Huffman encoding
*/
build_code(q[1], c, 0);
}
void encode(const char *s, char *out)
{
while (*s) {
strcpy(out, code[*s]);
out += strlen(code[*s++]);
}
}
void decode(const char *s, node t)
{
node n = t;
while (*s) {
if (*s++ == '0') n = n->left;
else n = n->right;
if (n->c) putchar(n->c), n = t;
}
putchar('\n');
if (t != n) printf("garbage input\n");
}
int main(void)
{
const char *str = "this is an example for huffman encoding";
char buf[1024];
init(str);
for (int i = 0; i < 128; i++)
if (code[i]) printf("'%c': %s\n", i, code[i]);
encode(str, buf);
printf("encoded: %s\n", buf);
printf("decoded: ");
decode(buf, q[1]);
return 0;
}
The C-code are based on Huffman coding.
Output should look like this:
' ': 000 'a': 1000 'c': 01101 'd': 01100 'e': 0101 'f': 0010 'g': 010000 'h': 1101 'i': 0011 'l': 010001 'm': 1111 'n': 101 'o': 1110 'p': 10011 'r': 10010 's': 1100 't': 01111 'u': 01110 'x': 01001 encoded: 0111111010011110000000111100000100010100001010100110001111100110100010 0100000101110100100001101011100010001011111000101000010110101101111001100001110 010000 decoded: this is an example for huffman encoding
As we see from the output, we consider only codes in which no code is also a prefix of a code for other characters. Such codes are called prefix. Prefix codes can always achieve the optimal data compression, and they are desirable because they simplify decoding such that no codeword is a prefix of any other, the codeword that begins an encoded file is unambiguous.
According to Shannon's source coding theorem, the entropy $H$ (in bits) is the weighted sum, across all symbols $a_i$ with non-zero probability $w_i$, of the information content of each symbol:
$$H = -\sum_{w_i} w_i log_2 w_i$$The entropy is a measure of the smallest codeword length that is theoretically possible for the given alphabet with associated weights. In this example, the weighted average codeword length is 2.25 bits per symbol, only slightly larger than the calculated entropy of 2.205 bits per symbol. So not only is this code optimal in the sense that no other feasible code performs better, but it is very close to the theoretical limit established by Shannon.- from wiki.
Actually, I wrote a separate page regarding this topic: Shannon Entropy.
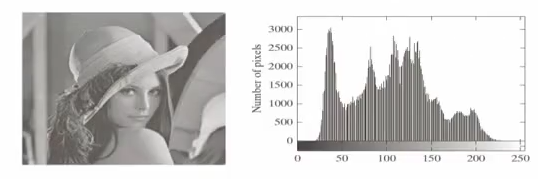
Answer is No!. As we can see from the pixel histogram on the right side, the Lena Reference Image is using different pixel values(0-255) with different frequencies, which we can utilize our Hoffman encoding.
Let's calculate how many bits we need to store $r_{87}, r_{128}, r_{186}, r_{255}$. $$\sum{p_r(r_k)I_2(r_k)} = 0.25\times2 + 0.47\times1 + 0.25\times3 + 0.03\times3 = 1.81 $$
So, we can achieve 1.81 bits rather than 8 bits for a pixel value!
*For more on heap-based implementation, please visit Heap-based Priority Queue.
Also, please visit http://www.bogotobogo.com/VideoStreaming/DigitalImageProcessing.php .
Ph.D. / Golden Gate Ave, San Francisco / Seoul National Univ / Carnegie Mellon / UC Berkeley / DevOps / Deep Learning / Visualization