Algorithms - Bellman Ford Shortest Path Algorithm - 2020

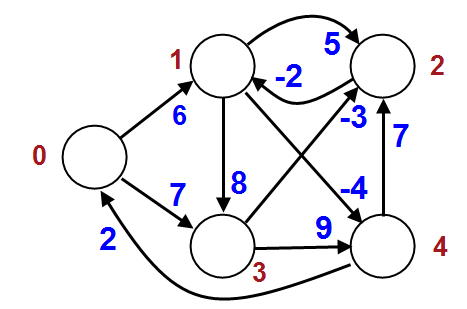
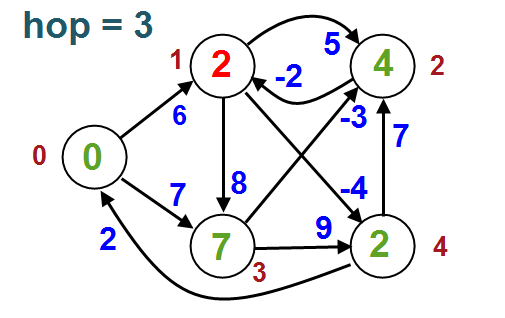
Like Dijkstra's Shortest Path, this Bellman-Ford is based on the relaxation technique, in which an approximation to the correct distance is gradually replaced by more accurate values until eventually reaching the optimum solution.

/*
procedure BellmanFord(list vertices, list edges, vertex source)
	// This implementation takes a vetext source
	// and fills distance array with shortest-path information

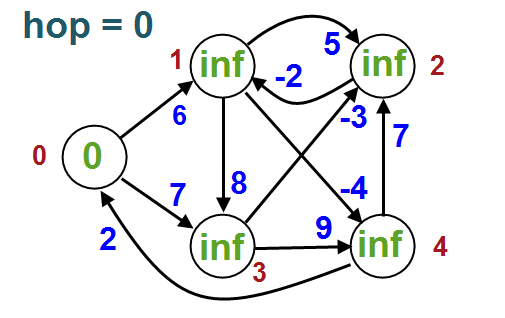
	// Step 1: initialize graph
	for each vertex v in vertices:
		if v is source 
			distance[v] := 0
		else 
			distance[v] := infinity

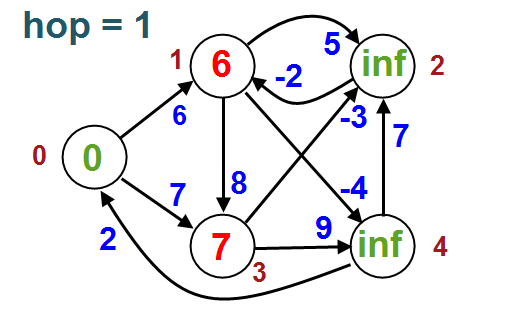
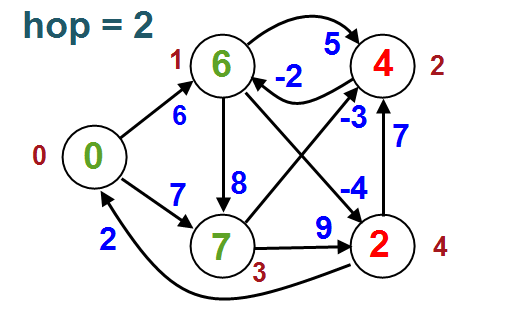
	// Step 2: relax edges repeatedly
	for i from 1 to size(vertices)-1:
		for each edge (u, v) with weight w in edges:
			if distance[u] + w < distance[v]:
				distance[v] := distance[u] + w

	// Step 3: check for negative-weight cycles
		for each edge (u, v) with weight w in edges:
			if distance[u] + w < distance[v]:
				error "Graph contains a negative-weight cycle"
*/

#include <iostream>

typedef struct {
    int u, v, w;
} Edge;
 
const int NODES = 5 ; /* the number of nodes */
int EDGES;            /* the number of edges */
Edge edges[32];       /* large enough for n <= 2^NODES=32 */
int d[32];            /* d[i] is the minimum distance from source node s to node i */
 
#define INFINITY INT_MAX
 
void BellmanFord(int src) 
{
    int i, j;
 
    for (i = 0; i < NODES; ++i) d[i] = INFINITY;
    d[src] = 0;
 
    for (i = 0; i < NODES - 1; ++i) {
        for (j = 0; j < EDGES; ++j) {
            if (d[edges[j].u] + edges[j].w < d[edges[j].v]) {
                d[edges[j].v] = d[edges[j].u] + edges[j].w;
	    }
	}
    }
	
    for (i = 0; i < NODES - 1; ++i) {
        for (j = 0; j < EDGES; ++j) {
            if (d[edges[j].u] + edges[j].w < d[edges[j].v]) {
                printf("Graph contains a negative-weight cycle\n");
		exit(1);
	    }
	}
    }
}
 
int main() 
{
    int i, j, w;
    int  k = 0;
 
    FILE *fin = fopen("path/BellmanFord.txt", "r");

    for (i = 0; i < NODES; ++i) {
        for (j = 0; j < NODES; ++j) {
            fscanf(fin, "%d", &w;);
            if (w != 0) {
                edges[k].u = i;
                edges[k].v = j;
                edges[k].w = w;
                k++;
            }
        }
    }
    fclose(fin);
    EDGES = k;

    for (i = 0; i < NODES; ++i) printf("Node %d\t", i );
    printf("\n--------------------------------------\n");

    int source_vertex = 0;
    BellmanFord(source_vertex);

    for (i = 0; i < NODES; ++i) printf("%d\t", d[i] );
 
    return 0;
}

Input file:

0   6   0   7   0
0   0   5   8  -4
0  -2   0   0   0
0   0  -3   0   9
2   0   7   0   0 

Output:

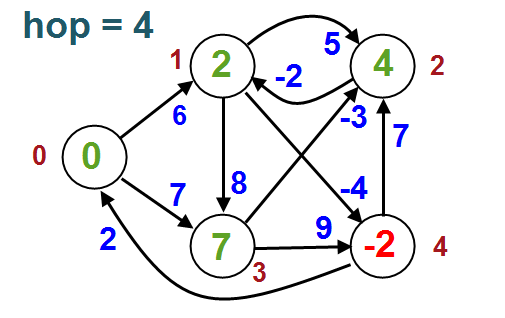
Node 0  Node 1  Node 2  Node 3  Node 4
--------------------------------------
0       2       4       7       -2