Algorithms - Quick Sort
Quicksort is the fastest known comparison-based sorting algorithm. it requirs O(n log n) steps, on average while works in place, which means minimal extra memory required. Quicksort is a recursive algorithm.
Quicksort sorts by employing a divide and conquer strategy to divide a list into two sub-lists.
The steps are:
- Pick an element, called a pivot, from the list.
- Reorder the list so that all elements with values less than the pivot come before the pivot, while all elements with values greater than the pivot come after it (equal values can go either way). After this partitioning, the pivot is in its rightful position. This is called the partition operation.
- Two cools facts about the partition:
- Linear (O(n)) in time, no extra memory since we use swaps.
- Reduces the problem size - divide and conquer.
- Recursively sort the sub-list of lesser elements and the sub-list of greater elements.
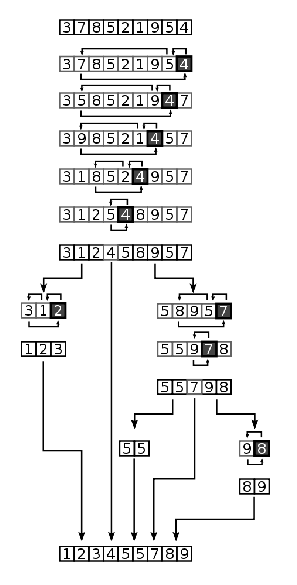
Full example of quicksort on a random set of numbers. The shaded element is the pivot. It is always chosen as the last element of the partition. However, always choosing the last element in the partition as the pivot in this way results in poor performance (O(n 2)) on already sorted lists, or lists of identical elements. Since sub-lists of sorted / identical elements crop up a lot towards the end of a sorting procedure on a large set, versions of the quicksort algorithm which choose the pivot as the middle element run much more quickly than the algorithm described in this diagram on large sets of numbers.
- The diagram and description above are from wiki
C++ code
#include <iostream>
#include <iomanip>
using namespace std;
#define SIZE 9
/* swap a[i] and a[j] */
void swap(int a[], int i, int j)
{
int temp;
temp = a[i];
a[i] = a[j];
a[j] = temp;
}
void print(const int arr[])
{
for(int i=0;i < SIZE; i++) {
cout << setw(3) << arr[i];
}
cout << endl;
}
/* sort arr[left]...arr[right] into increasing order */
void qsort(int a[], int left_index, int right_index)
{
int left, right, pivot;
if(left_index >= right_index) return;
left = left_index;
right = right_index;
// pivot selection
pivot = a[(left_index + right_index) /2];
// partition
while(left <= right) {
while(a[left] < pivot) left++;
while(a[right] > pivot) right--;
if(left <= right) {
swap(a,left,right);
left++; right--;
}
print(a);
}
// recursion
qsort(a,left_index,right);
qsort(a,left,right_index);
}
int main()
{
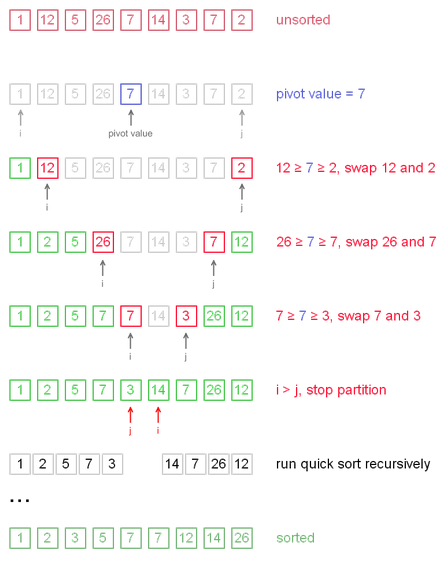
int a[SIZE]={1, 12, 5, 26, 7, 14, 3, 7, 2};
print(a);
qsort(a,0,SIZE-1);
}
Output:
1 12 5 26 7 14 3 7 2 1 2 5 26 7 14 3 7 12 1 2 5 7 7 14 3 26 12 1 2 5 7 3 14 7 26 12 1 2 5 7 3 14 7 26 12 1 2 3 7 5 14 7 26 12 1 2 3 7 5 14 7 26 12 1 2 3 7 5 14 7 26 12 1 2 3 5 7 14 7 26 12 1 2 3 5 7 7 14 26 12 1 2 3 5 7 7 14 12 26 1 2 3 5 7 7 12 14 26
Here is more detailed output from the run:
1 12 5 26 7 14 3 7 2 1 12 5 26 7 14 3 7 2 pivot element = 7 swap(12,2) 1 2 5 26 7 14 3 7 12 swap(26,7) 1 2 5 7 7 14 3 26 12 swap(7,3) 1 2 5 7 3 14 7 26 12 1 2 5 7 3 14 7 26 12 1 2 5 7 3 pivot element = 5 swap(5,3) 1 2 3 7 5 14 7 26 12 1 2 3 7 5 14 7 26 12 1 2 3 pivot element = 2 swap(2,2) 1 2 3 7 5 14 7 26 12 7 5 pivot element = 7 swap(7,5) 1 2 3 5 7 14 7 26 12 14 7 26 12 pivot element = 7 swap(14,7) 1 2 3 5 7 7 14 26 12 14 26 12 pivot element = 26 swap(26,12) 1 2 3 5 7 7 14 12 26 14 12 pivot element = 14 swap(14,12) 1 2 3 5 7 7 12 14 26
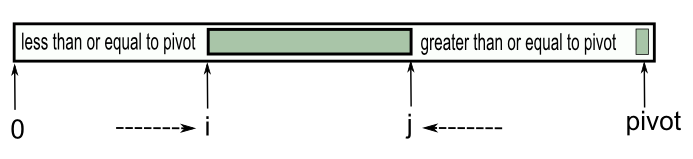
Quicksort is a divide and conquer algorithm which relies on a partition operation: to partition an array, we choose an element, called a pivot, move all smaller elements before the pivot, and move all greater elements after it. This can be done efficiently in linear time and in-place. We then recursively sort the lesser and greater sublists. Efficient implementations of quicksort (with in-place partitioning) are typically unstable sorts and somewhat complex, but are among the fastest sorting algorithms in practice. Together with its modest O(log n) space usage, this makes quicksort one of the most popular sorting algorithms, available in many standard libraries. The most complex issue in quicksort is choosing a good pivot element; consistently poor choices of pivots can result in drastically slower (O(n^2)) performance, but if at each step we choose the median as the pivot then it works in O(n log n).
In the previous section, we used the pivot from the middle index of the array, and the way of partitioning was ambiguous. So, in this section, I take the most traditional approach and keep the partition routine separate while using the right most element as a pivot element.
#include <iostream>
using namespace std;
template<class T>
void exchg(T &a, T &b)
{
T tmp = b;
b = a;
a = tmp;
}
template<class T>
int partition(T a[], int left, int right)
{
T pivot = a[right];
int i = left - 1;
int j = right;
for(;;)
{
while(a[--j] > pivot);
while(a[++i] < pivot);
if(i >= j) break;
exchg(a[i], a[j]);
}
exchg(a[right], a[i]);
return i;
}
template<class T>
void quick(T a[], int left, int right)
{
if(left >= right) return;
int p = partition(a, left, right);
quick(a, left, p-1);
quick(a, p+1, right);
}
int main()
{
char a[] = {'A','S','O','R','T','I','N','G',
'E','X','A','M','P','L','E'};
quick(a, 0, sizeof(a)/sizeof(a[0])-1);
return 0;
}
1. What is the running time of a quicksort on an input array of size n that is already sorted?
The pivot we choose for this case is the index 0.
Answer: O(n^2)
That's because the partition should look up the array elements in each of recursion level: n, n-1, n-2,... 1
This gives the running time n+(n-1)+(n-2)+...+1 ~ O(n^2) - This is the worst case.
2. If we choose median element for every recursive call, what's the running time?
Answer: O(nlog(n)). And this is the best we can get from Quicksort.
3. Quicksort is strongly dependent of the choice of the pivot. Then, how to choose pivot?
Answer: Use random pivot for every recursive call.
- 25-75% split almost guarantees nlog(n).
- That means half of elements give 25-75% split.
Ph.D. / Golden Gate Ave, San Francisco / Seoul National Univ / Carnegie Mellon / UC Berkeley / DevOps / Deep Learning / Visualization