Algorithms - Hashing
Hash table (hash map) is a data structure which basically maps unique keys to associated values. The hash table is an array-based data structure, which uses hash function to convert the key into the index of an array element, where associated value is to be sought.
Many applications require a dynamic set that support only the dictionary (table) operations such as insert, search, and delete. A hash table is an effective data structure for implementing dictionaries. Although searching for an element in a hash table can take as long as searching for an element in a linked list - O(n) time in the worst case - in practice, hashing performs extremely well.
Under reasonable assumptions, the average time to search for an element in a hash table is O(1). But this doesn't mean only one comparison will be made. It means that no matter how large the data set, the number of comparisons will remain the same. We can compare this with linked list (O(n)) and with binary search tree (O(nlog(n)).
A hash table generalizes the simpler notion of an ordinary array. Directly addressing into an ordinary array makes effective use of our ability to examine an arbitrary position in an array in O(1) time.
Hashing is the extension of key-indexed search method, and it takes completely different approach to search. Rather than navigating through dictionary data structures by comparing search keys with keys in items, hashing is trying to reference items into table directly by doing arithmetic operations to transform keys into table addresses.
When the number of keys actually stored is small relative to the total number of possible keys, hash table becomes an effective alternative to directly addressing an array, since a hash table typically uses an array of size proportional to the number of keys actually stored. Instead of using the keys as an array index directly, the array index is computed from the key.
There are two main concerns when implementing hash-based search: hash function and collision (when two keys map to the same bin). Improper hash function may lead to poor distribution of the keys which has the following consequences: (a) wasting space - many slots in the hash table may be unused. (b) performance hit - there will be many collisions where the keys map into the same slot.
So, implementing hash table involves couple of ideas such as
- separate chaining as a way to handle collisions
in which more than one key map to the same array index
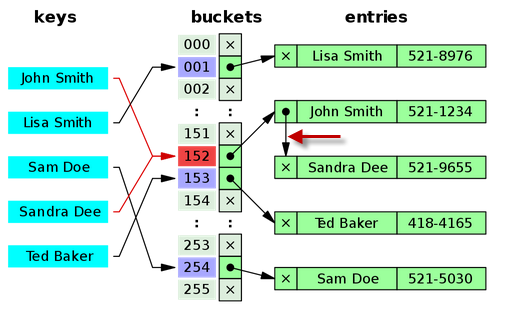
picture from wiki
- keep linked list in each bucket
- given a key/object x, perform insert/delete/lookup in the list in array[hash(x)]
- if space is crucial, then we may have to use open addressing.
- when load factor is larger than 1, where load factor, α = (# of objects in hash table)/(# of buckets in hash table)
- open addressing which is another way to deal with collisions. (only one object per bucket)
- linear probing (look up consecutively)
- double hashing - use two hashing functions
- deletion is trickier than the chaining case which uses linked list.
- perfect hashing which gives us O(1) worst-case search time.
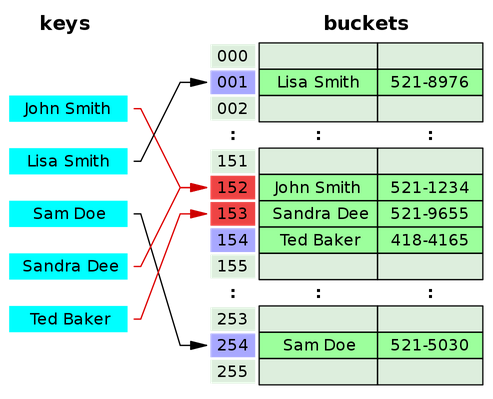
picture from wiki
Check an example for Hash Table in C++.
The following example is builds hash map from linux dictionary, /usr/share/dict/words, storing words staring with "x" or "X". The map has dynamically allocated 128 tables. If each table has more than one element, it uses chaining.
#include <iostream>
#include <fstream>
#include <string>
using namespace std;
const int TABLE_SIZE = 128;
struct TableList {
string key;
int value;
struct TableList *next;
};
unsigned hash_function(string);
unsigned rehash(unsigned);
class HashMap
{
private:
TableList **table;
public:
HashMap()
{
table = new TableList*[TABLE_SIZE];
for(int i = 0; i < TABLE_SIZE; i++) table[i] = NULL;
}
struct TableList* lookup(string s)
{
struct TableList *tp;
for(tp = table[hash_function(s)]; tp != NULL; tp = tp->next)
if((tp->key).compare(s) == 0) return tp; // found
return NULL; // not found
}
void put(string key, int value) {
struct TableList *tp;
unsigned hash;
// not found
if(!(tp = lookup(key))) {
tp = new TableList;
tp->key = key;
tp->value = value;
hash = hash_function(key);
tp->next = table[hash];
table[hash] = tp;
// it's already there
} else {
tp->key = key;
tp->value = value;
hash = hash_function(key);
table[hash] = tp;
}
}
~HashMap()
{
for (int i = 0; i < TABLE_SIZE; i++)
if (table[i] != NULL) delete table[i];
delete[] table;
}
void showMap()
{
struct TableList *tp;
for (int i = 0; i < TABLE_SIZE; i++) {
tp = table[i];
if(tp)
cout << "table[" << i << "] " << tp->key << "(" << tp->value << ")";
else
continue;
while(tp) {
cout << "->" << tp->key << "(" << tp->value << ")";
tp = tp->next;
}
cout << endl;
}
}
};
unsigned hash_function(string s)
{
unsigned hash = 0;
for (int i = 0; i < s.length(); i++)
hash = s[i] + 31*hash;
return hash % TABLE_SIZE;
}
int main()
{
HashMap m;
string line;
//ifstream dict_reader("/usr/share/dict/words");
ifstream dict_reader("C:/TEST/linux.words");
if( !dict_reader ) {
cout << "Error opening input file - dict " << endl ;
exit(1) ;
}
int count = 0;
while(getline(dict_reader,line)) {
if((line[0] >= 'x' && line[0] < 'y') || (line[0] >= 'X' && line[0] < 'Y') ) {
m.put(line,count++);
}
}
m.showMap();
return 0;
}
We need to define a function to compute the key for a string, s, in the list. One goal for the key function is to produce as many different values as possible but it is not necessary for the values to all be unique. One of the most popular techniques is to produce a value based on each piece of information from the original string:
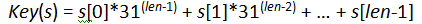
where s[i] is the i-th character, and len is the length of the string s.
Then the next thing is to construct the hash table. We have n strings but what should be the size of the hash table?
As an ideal case, the size of the hash table (TABLE_SIZE) could be equal to n tables where the hash function is a one-to-one function. But this may not happen in real life case. But we need to try to have a hash table that has as few empty tables as possible. If our hash function distributes the keys evenly, we may achieve reasonable success by selecting an array size approximately as large as the collection. A perfect hash function is one that guarantees no collision, but this happens rarely.
Another thing we need to decide is the strategy for handling collision. The approach we took in the above code was to store a pointer to a list of entries in each slot of the primary hash table, rather than a single object, known as chaining.
Also note the way how the delete is used in ~HashMap(). (see Deleting a Pointer to a Pointer (Array of objects))
The output looks like this:
table[0] xylitols(533)->xylitols(533)->xylidic(523)->xx(498)->xerophile(320)->xerodermic(299).... table[1] Xylophagidae(573)->Xylophagidae(573)->xiphoid(410)->Xerxes(354) table[2] xyl-(505)->xyl-(505)->xanthoproteic(106) table[3] Xymenes(613)->Xymenes(613)->xerus(352)->xero-(293)->xanthopicrin(104)->xanthocobaltic(62) table[4] xysters(623)->xysters(623)->Xina(374) table[5] xerophil(319)->xerophil(319)->Xanthomelanoi(86) table[6] xystos(626)->xystos(626)->xiphydriid(429)->xenopeltid(232)->xanthelasma(22) table[7] xysti(624)->xysti(624)->xylenyl(519)->Xmas(437) ..... table[122] Xylariaceae(511)->Xylariaceae(511)->xr(465)->xenogenesis(209)->xanthoxylin(127)->xanthates(16) table[123] xylans(508)->xylans(508)->xs(473)->Xiphura(427)->xiphosure(422)->xiphiid(391)->..... table[124] xystoi(625)->xystoi(625)->xurel(488)->XT(478)->XIM(369)->xeroxes(349)->Xenurus(276)->.... table[125] xylophagid(572)->xylophagid(572)->XVIEW(492)->xu(485)->xoana(451)->Ximenia(373)->.... table[126] xoanona(453)->xoanona(453)->XMS(442)->Xian(362)->xeroma(305)->xerodermia(298)->Xanthorrhiza(115) table[127] xylotomous(603)->xylotomous(603)->xw(495)->xeroprinting(333)->xeric(290)->xeno-(185)->xenelasy(173)
#include <iostream>
using namespace std;
class HashEntry
{
private:
int key;
int value;
public:
HashEntry(int key, int value)
{
this->key = key;
this->value = value;
}
int getKey()
{
return key;
}
int getValue()
{
return value;
}
};
const int TABLE_SIZE = 5;
class HashMap
{
private:
HashEntry **table;
public:
HashMap()
{
table = new HashEntry*[TABLE_SIZE];
for (int i = 0; i < TABLE_SIZE; i++)
table[i] = NULL;
}
int get(int key)
{
int hash = (key % TABLE_SIZE);
while (table[hash] != NULL && table[hash]->getKey() != key)
hash = (hash + 1) % TABLE_SIZE;
if (table[hash] == NULL)
return -1;
else
return table[hash]->getValue();
}
void put(int key, int value)
{
int hash = (key % TABLE_SIZE);
int hashCount = 0;
if(table[hash] != NULL)
// Same hash, but the key is different, use another hash
while (table[hash] != NULL && table[hash]->getKey() != key) {
hash = (hash + 1) % TABLE_SIZE;
// if not found, give up
if(hashCount++ == TABLE_SIZE) break;
}
// Same hash, delele old and make a new one
if (table[hash] != NULL)
delete table[hash];
table[hash] = new HashEntry(key, value);
}
~HashMap()
{
for (int i = 0; i < TABLE_SIZE; i++)
if (table[i] != NULL)
delete table[i];
delete[] table;
}
};
int main()
{
HashMap *myMap = new HashMap;
int key;
for(int i = 0; i < TABLE_SIZE; i++) {
key = i*10;
myMap->put(key, key*10);
cout << key << ": " << myMap->get(key) << endl;
}
for(int i = 0; i < TABLE_SIZE; i++) {
key = i*20;
myMap->put(key, key*100);
cout << key << ": " << myMap->get(key) << endl;
}
return 0;
}
Though there are several ways of implementing maps, STL map is usually implemented using balanced binary search trees, more specifically they are red-black trees.
But the unordered_map is implemented by using hash table (hashing). The unordered_map is not C++ standard yet, and we need to use boost.
So, how do we know which one to use?
- map - if we need to look up based on a value.
- unordered_map - if we need to do a lot of lookup in a large map and we do not need an ordered traversal while we can find a good hash function for our key type.
What is the difference between a tree and a hashtable?
We can describe the difference in two ways:
- behavior, where behavior describes the functionality as well as the performance.
- Hash Table - constant time inserts, searches, and deletes
There are more things to consider such as sizing a hash table appropriately, the effect of resizing a hash table, and how to handle collisions (two objects hash to the same value). - Tree - log(n) inserts, log(n) searches, and log(n) deletes
To keep its intended performance, the tree should maintain its balance. Great deal of efforts must be expended in order to keep a tree balanced, which complicates its implementation.
- Hash Table - constant time inserts, searches, and deletes
- implementation details
- Hash Table - A hash table is a contiguous region of memory, similar to an array, in which objects are hashed using hash function into an index in that memory.
- Tree - trees store its data in a hierarchical tree
Pros and cons of Hashtable and Tree.
- Hash Table
- Hash table requires more memory than is needed to hold its data. In general, a hash table should not be more than 75% - 80% full. This means that if we want to hold 100 element, we need to have a hash table that can hold 125 - 133 elements.
- Rehashing is very expensive operation that requires n operations. Our constant time insert becomes of order O(n) when we need rehasing, which is far worse than the performance of a tree.
- There is no way to extract objects in any natural order. The order is determined by where the hashing algorithm inserts the objects, not on any natural order.
- Tree
- Trees can save memory because they only use the amount of memory needed to hold its items.
- No need for rehashing because trees can grow and shrink as needed, so order is always less than n.
- It is simple to extract items in their natural order.
Choose hashtable if we know approximately how many items to maintain in our collection and do not want to extract items in a natural order, then hash tables are our best choice because they offer constant time insertion, search, and deletion.
However, go for tree, if memory is tight and do not know how many items to store in memory, and/or want to extract objects in a natural order. In other words, if items will be consistently added and removed and do not know how many items will be stored in our collection, then we might be willing to accept O(log n) search time (instead of constant time from hashtable) to avoid potential rehashing at runtime.
- Constant operation for search/delete/insert, and we know the size of items, not in memory tight situation, hash table. Order - constant, rehashing (n).
- If order is important, tree. Order - log(n), never exceeds n.
- Frequent insertion/deletion, and not many search, linked list. Order - insert/delete (constant), search (n).
The following example demonstrates that it's quite easy to get collision when we implement the hash function. Even with tiny set of data for each bucket, the collision can starts to be happening.
Someone told me that if there are 23 people in a room there's a 50/50 chance that two of them will have the same birthday.
How can that be?
- Avoiding the collision. Let's count the probability of the case when all the 23 people take different birthday.
- The first person can take all 365 days. So, any day can be taken, and the probability of no collision is 100%. In other words, the it's 1 = 365/365
- The 2nd person can take one less than 365, so the chance of no-collision is 364/365.
- The probability of no-collision of the two people's birthdays is (365/365)*(364/365).
- If we do this for all 23 people, it should look like this: (365/365)*(364/365)*...(343/365) ~ 0.49
- Actually, it is equal to (nPr)/(365^r) = (365P23)/(365^23).
- So, collision chance would be 1-0.49=0.51=51% with just 23 people.
- The claim is true!
- With only 57 people, collision chance reaches 99%.
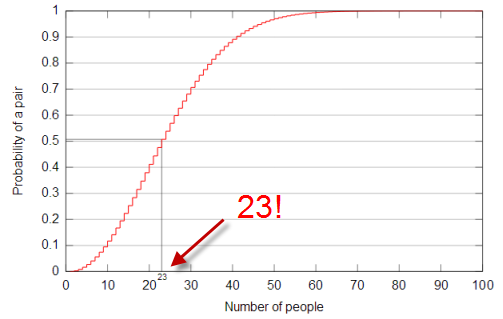
Picture from wiki
Here, we assume we're using hash table with chaining.
insert is O(1) if we insert a new object at front of the list in A[hash(x)].
In general, for the insert/delete operation, the running time is O(list length). The list length could be in the range of m/n to m where m is the number of objects, n is the number of buckets.
The performance of the hash hash table depends on the choice of hash function!
Properties of a Good Hash function
- should lead to good performance by spreading data uniformly across the buckets. We can achieve this by using completely random hashing.
- should be easy to store and should be very fast to evaluate the hash function.
- How to choose # of buckets, n?
- choose n to be a prime within constant factor of # of objects in table.
- not too close to a power of 2 or 10.
A Bloom filter is a data structure designed to tell us, super-fast and memory-efficiently, whether an element is present in a set.
Application:
- early spell checkers
- list of forbidden passwords
- network routers
Ph.D. / Golden Gate Ave, San Francisco / Seoul National Univ / Carnegie Mellon / UC Berkeley / DevOps / Deep Learning / Visualization